题目内容
已知：如图，△ABC内接于圆，AB=AC，D为延长线上一点，AD交圆于E．求证：AB2=AD•AE．考点：相似三角形的判定与性质,圆周角定理
专题：证明题
分析：如图，作辅助线；证明△ABE∽△ADB，列出比例式，即可解决问题．
解答：
证明：如图，连接BE；
∵AB=AC，
∴∠B=∠ACB；
∵∠AEB=∠ACB，
∴∠AEB=∠B，而∠BAE=∠BAD，
∴△ABE∽△ADB，
∴AB：AD=AE：AB，
∴AB2=AD•AE．
证明：如图，连接BE；∵AB=AC，
∴∠B=∠ACB；
∵∠AEB=∠ACB，
∴∠AEB=∠B，而∠BAE=∠BAD，
∴△ABE∽△ADB，
∴AB：AD=AE：AB，
∴AB2=AD•AE．
点评：该题主要考查了圆周角定理、相似三角形的判定及其性质定理的应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知正六边形的边长是2，则该正六边形的边心距是（ ）
| A、1 | ||||
B、
| ||||
| C、2 | ||||
D、
|
如图，⊙O的直径AB与弦CD相交于E，
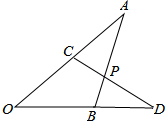如图，已知AC=BD，∠A=∠D，AB、CD交于点P，求证：点P到OA、OD的距离相等．
如图，在△ABC中，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论：