题目内容
 如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.
如图,在等腰直角三角形ABC中,∠ACB=90°,D为斜边AB上一点,连接CD,过点A、B分别向CD作垂线,垂足分别为点F、E,试判断AF、BE与EF之间的数量关系,并证明你的结论.考点:全等三角形的判定与性质
专题:
分析:求出∠BEC=∠CFA=90°,∠CBE=∠ACF,根据AAS推出△BEC≌△CFA,根据全等三角形的性质得出BE=CF,AF=CE,即可得出答案.
解答:答:AF-BE=EF,
证明:∵BE⊥CE,AF⊥CE,∠ACB=90°,
∴∠BEC=∠CFA=90°,
∴∠BCE+∠ACF=90°,∠BCE+∠CBE=90°,
∴∠CBE=∠ACF,
在△BEC和△CFA中,
,
∴△BEC≌△CFA(AAS),
∴BE=CF,AF=CE,
∴EF=CE-CF=AF-BE,
即AF-BE=EF.
证明:∵BE⊥CE,AF⊥CE,∠ACB=90°,
∴∠BEC=∠CFA=90°,
∴∠BCE+∠ACF=90°,∠BCE+∠CBE=90°,
∴∠CBE=∠ACF,
在△BEC和△CFA中,
|
∴△BEC≌△CFA(AAS),
∴BE=CF,AF=CE,
∴EF=CE-CF=AF-BE,
即AF-BE=EF.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△BEC≌△CFA,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论:
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论:①AD上任意一点到AB、AC的距离相等;②BD=CD;③S△ADB=S△ADC;④∠BDE=∠CDF
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,若∠D=45°,则∠PCA=( )| A、50° | B、57.5° |
| C、60° | D、67.5° |
台风是一种破坏性极大的自然灾害,气象台为预报台风,首先确定它的位置,下列说法能确定台风位置是( )
| A、北纬26°,东经133° |
| B、西太平洋 |
| C、距离台湾300海里 |
| D、台湾与冲绳岛之间 |
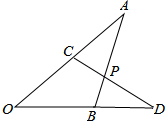 如图,已知AC=BD,∠A=∠D,AB、CD交于点P,求证:点P到OA、OD的距离相等.
如图,已知AC=BD,∠A=∠D,AB、CD交于点P,求证:点P到OA、OD的距离相等.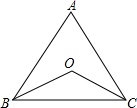 如图,在△ABC中,∠ABC,∠ACB的角平分线相交于点O,
如图,在△ABC中,∠ABC,∠ACB的角平分线相交于点O,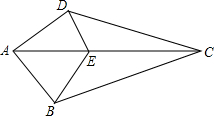 如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC.
如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC=∠BEC.