题目内容
12.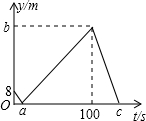 甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
分析 由函数图象可以分别求出甲的速度为4米/秒,乙的速度为5米/秒,就可以求出乙追上甲的时间a的值,b表示跑完全程的距离应该为500米,c表示乙出发后多少时间甲走完全程就用甲走完全程的时间-2就可以得出结论.
解答 解:由题意及函数图象可以得出:
甲的速度为:8÷2=4(米/秒),
乙的速度为:500÷100=5(米/秒),
a=8÷(5-4)=8(秒);
b=500-4×102=92(米),
c=500÷4-2=123(秒).
则(1)(2)正确.
故选B.
点评 本题考查了行程问题的数量关系的运用,追击问题在实际生活中的运用,一次函数的图象的性质的运用,解答时认真分析函数图象的意义是解答本题的关键.

练习册系列答案
相关题目
17.若一个多边形的内角和是外角和的3倍,则这个正多边形的边数是( )
| A. | 10 | B. | 9 | C. | 8 | D. | 6 |
1.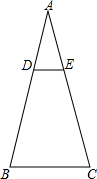 如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
 如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )| A. | 1:4 | B. | 1:9 | C. | 3:4 | D. | 8:9 |
2. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB边上,OM、ON分别交边AC、BC于点P、Q,∠MON绕点O任意旋转.当$\frac{OA}{OB}=\frac{1}{2}$时,$\frac{OP}{OQ}$的值为 ______;当$\frac{OA}{OB}=\frac{1}{n}$时,$\frac{OP}{OQ}$的值为 ______(用含n的式子表示).其中正确的选项是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB边上,OM、ON分别交边AC、BC于点P、Q,∠MON绕点O任意旋转.当$\frac{OA}{OB}=\frac{1}{2}$时,$\frac{OP}{OQ}$的值为 ______;当$\frac{OA}{OB}=\frac{1}{n}$时,$\frac{OP}{OQ}$的值为 ______(用含n的式子表示).其中正确的选项是( )
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB边上,OM、ON分别交边AC、BC于点P、Q,∠MON绕点O任意旋转.当$\frac{OA}{OB}=\frac{1}{2}$时,$\frac{OP}{OQ}$的值为 ______;当$\frac{OA}{OB}=\frac{1}{n}$时,$\frac{OP}{OQ}$的值为 ______(用含n的式子表示).其中正确的选项是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB边上,OM、ON分别交边AC、BC于点P、Q,∠MON绕点O任意旋转.当$\frac{OA}{OB}=\frac{1}{2}$时,$\frac{OP}{OQ}$的值为 ______;当$\frac{OA}{OB}=\frac{1}{n}$时,$\frac{OP}{OQ}$的值为 ______(用含n的式子表示).其中正确的选项是( )| A. | $\frac{\sqrt{3}}{2};\frac{\sqrt{3}}{n}$ | B. | $\frac{\sqrt{3}}{n};\frac{\sqrt{3}}{n}$ | C. | $\frac{\sqrt{3}}{2};\sqrt{3}$ | D. | $\sqrt{3}$;$\frac{\sqrt{3}}{n}$ |
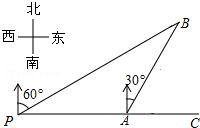 如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离.
如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离. 如图,已知△ABC,其中AB=AC.
如图,已知△ABC,其中AB=AC.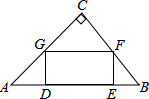 如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6.
如图,在直角三角形ABC中,∠C=90°,矩形DEFG的四个顶点都在△ABC的边上,已知:AC=8,BC=6. 已知抛物线y=$\frac{1}{2}$x2+2(m+1)x-m+1与x轴交于点A、B,与y轴交于点C,其对称轴是直线x=4.
已知抛物线y=$\frac{1}{2}$x2+2(m+1)x-m+1与x轴交于点A、B,与y轴交于点C,其对称轴是直线x=4.