题目内容
1.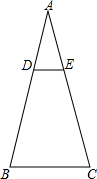 如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )| A. | 1:4 | B. | 1:9 | C. | 3:4 | D. | 8:9 |
分析 因为DE∥BC,所以可得△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方解答即可.
解答 解:∵D、E分别是△ABC的AB、AC边上的点,DE∥BC
∴△ADE∽△ABC
∵AE:EC=1:2
∴AE:AC=1:3
∴S△ADE:S△ABC=1:9
∴$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=$\frac{8}{9}$.
故选D.
点评 本题考查了相似三角形的面积的比等于相似比的平方的运用,熟记定理是解题的关键.

练习册系列答案
相关题目
12.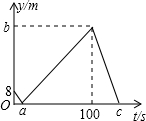 甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
 甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )
甲、乙两人在一条长为500m的直线跑道上同起点、同向匀速跑步,已知甲先出发2s后乙再出发,先到终点的人原地休息,如图表示的是甲、乙两人之间的距离y(m)与乙出发的时间t(s)的函数关系,给出以下结论:①a=8;②b=92;③c=23,其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
16. 如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
 如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
如图,等边三角形ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
6.方程组$\left\{\begin{array}{l}{3x-5y=6,①}\\{2x-3y=4,②}\end{array}\right.$将②×3-①×2得( )
| A. | -3y=2 | B. | 4y+1=0 | C. | y=0 | D. | x-2y=2 |
13.在平面直角坐标系中,点P(-3,a2+1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |




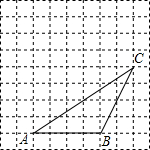 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.