Question

20．如图，设AD是△ABC的中线，△ABD，△ADC的外心分别为E、F，直线BE与CF交于点G，若DG=$\frac{1}{2}$BC，求证：∠ADG=2∠ACG．

Answer 1

分析 首先证明∠AFG=2∠ACF，再证明A、D、F、G四点共圆，推出∠ADG=∠AFG即可解决问题．

解答 证明：连接AG，AE，AF，DE，DF，EF．
∵DB=CD，DG=$\frac{1}{2}$BC，
∴BD=DC=DG，
∴∠BGC=90°，
∴∠GBC+∠GCD=90°，
∵E、F是△ABD，△ADC的外心，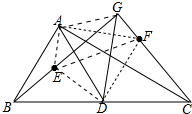
∴EB=EA=ED，FD=FC=FA，
∴∠EBD=∠EDB，∠FDC=∠FCD，
∴∠EDC+∠FDC=90°，
∴∠EDF=90°，
在△EFA和△EFD中，
$\left\{\begin{array}{l}{EF=EF}\\{AE=ED}\\{AF=FD}\end{array}\right.$，
∴△EFA≌△EFD，
∴∠EAF=∠EDF=90°，
∴A、E、D、F四点共圆，E、D、F、G四点共圆，
∴A、E、D、F、G五点共圆，
∴∠ADG=∠AFG，
∵FA=FC，
∠FAC=∠FCA，
∠AFG=∠FAC+∠FCA=2∠FCA，
∴∠ADG=2∠ACG．

点评 本题考查三角形外接圆、外心、四点共圆等知识，解题的关键是学会添加辅助线构造全等三角形解决问题，证明ADFG四点共圆是解题突破点，题目有一定的难度，属于中考压轴题．