Question

10．在⊙O中，AB为⊙O的直径，AC是弦，P为直径BA延长线上的一动点，CP与⊙O相切，PA=AC，点F为直径AB上一点，延长CF交⊙O于点M
（1）如图1，求证：∠AOC=60°；
（2）如图2，当∠AFM+∠ABM=90°，BC=$\sqrt{3}$时，求OF的长．

Answer 1

分析 （1）由AP=AC，推出∠P=∠ACP，由∠P+∠POC=90°，∠PCA+∠ACO=90°，推出∠POC=∠ACO，推出OA=OC=AC，由此即可解决问题．
（2）由∠MAB+∠ABM=90°，∠AFM+∠ABM=90°，推出∠MAF=∠MFA，只要证明BC=BF即可解决问题．

解答 解：（1）如图1中，

∵PC是⊙O切线，
∴PC⊥OC，
∴∠PCO=90°，
∵AP=AC，
∴∠P=∠ACP，
∵∠P+∠POC=90°，∠PCA+∠ACO=90°，
∴∠POC=∠ACO，
∴AC=AO=CO，
∴△ACO是等边三角形，
∴∠AOC=60°．

（2）如图2中，连接BC、AM．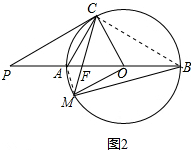

∵AB是直径，
∴∠AMB=90°，
∵∠MAB+∠ABM=90°，∠AFM+∠ABM=90°，
∴∠MAF=∠MFA，
∵∠MAB=∠MCB，∠AFM=∠CFB，
∴∠BCF=∠BFC，
∴BC=BF，
在Rt△ACB中，∠CAB=60°，BC=$\sqrt{3}$，
∴sin60°=$\frac{BC}{AB}$，
∴$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{AB}$，
∴AB=2，OA=OB=1，
∴AF=AB-BF=2-$\sqrt{3}$，
∴OF=OA-AF=1-（2-$\sqrt{3}$）=$\sqrt{3}$-1．

点评 本题考查圆的综合题、等边三角形的判定和性质、锐角三角函数等知识，解题的关键是熟练应用这些知识解决问题，学会添加常用辅助线，充分利用圆的有关性质解决问题，属于中考压轴题．