题目内容
5.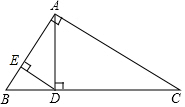 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是( )| A. | $\frac{21}{2}$ | B. | $\frac{{\sqrt{15}}}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{{3\sqrt{5}}}{2}$ |
分析 先证明Rt△ACD∽Rt△DAE,根据对应边成比例得出AD:AC=DE:AD,从而得出AC的长,再由勾股定理得出CD即可.
解答 解:∵AD⊥BC,DE⊥AB,
∴∠ADC=∠AED=90°,
∵∠BAC=90°,
∴∠DAE=∠C,
∴Rt△ACD∽Rt△DAE,
∴$\frac{AD}{AC}$=$\frac{DE}{AD}$,
∵AD=3,DE=2,
∴$\frac{3}{AC}$=$\frac{2}{3}$,
∴AC=$\frac{9}{2}$,
在Rt△ACD中,CD2+AD2=AC2,
∴CD=$\sqrt{(\frac{9}{2})^{2}-{3}^{2}}$=$\frac{3\sqrt{5}}{2}$,
故选D.
点评 本题考查了相似三角形的判定和性质,掌握判定三角形相似的方法以及勾股定理是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.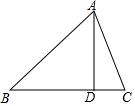 如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
 如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )
如图,在△ABC中,AD⊥BC,垂足为D,若AD=4,∠B=45°,△ABC的面积为12,则AC边的长是( )| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $3\sqrt{2}$ |
14.根据如图所示,对a、b、c三种物体的重量判断正确的是( )


| A. | a<b | B. | b<c | C. | a>c | D. | a<c |
15.对于$\sqrt{5}$-2,下列说法中正确的是( )
| A. | 它是一个无理数 | B. | 它比0小 | ||
| C. | 它不能用数轴上的点表示出来 | D. | 它的相反数为$\sqrt{5}$+2 |
 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.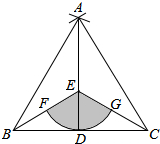 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.  如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.