题目内容
20．在实数：-$\sqrt{2}$，3.14159，$\root{3}{27}$，π，1.010010001…，4.$\stackrel{•}{2}$$\stackrel{•}{1}$，$\frac{1}{3}$中，无理数有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解答 解：-$\sqrt{2}$，π，1.010010001…是无理数，
故选：A．
点评 此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
11．对于任意实数x，下列各式中一定成立的是（ ）
| A． | $\sqrt{{x}^{2}-1}$=$\sqrt{x-1}$•$\sqrt{x+1}$ | B． | $\sqrt{{（x+1）}^{2}}$=x+1 | C． | $\sqrt{（-4）•（-x）}$=$\sqrt{-4}$•$\sqrt{-x}$ | D． | $\sqrt{3{6x}^{4}}$=6x2 |
如图，在?ABCD中，∠D=45°，∠CAD=35°，求∠B和∠BAC的度数．
15．不等式4+2x＞0的解集是（ ）
| A． | 2x＞4 | B． | x＞2 | C． | x＞-2 | D． | x＜-2 |
5．a、b、c为△ABC三边，不是直角三角形的是（ ）
| A． | a2=c2-b2 | B． | a=6，b=10，c=8 | ||
| C． | ∠A：∠B：∠C=3：4：5 | D． | a=8k，b=17k，c=15k |
9．下列关于$\sqrt{8}$的说法中，错误的是（ ）
| A． | $\sqrt{8}$是8的算术平方根 | B． | 2＜$\sqrt{8}$＜3 | ||
| C． | $\sqrt{8}$=$±2\sqrt{2}$ | D． | $\sqrt{8}$是无理数 |
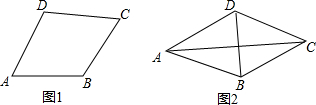类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．