题目内容
5.a、b、c为△ABC三边,不是直角三角形的是( )| A. | a2=c2-b2 | B. | a=6,b=10,c=8 | ||
| C. | ∠A:∠B:∠C=3:4:5 | D. | a=8k,b=17k,c=15k |
分析 利用勾股定理的逆定理判断A、B、D选项,用直角三角形各角之间的关系判断C选项.
解答 解:A、∵a2=b2-c2,∴a2+c2=b2,故本选项正确;
B、∵62+82=102,∴a2+b2=c2,故本选项正确;
C、∵∠A:∠B:∠C=3:4:5,∴设∠A=3x,则∠B=4x,∠C=5x,
∵∠A+∠B+∠C=180°,即3x+4x+5x=180°,解得,x=15°,
∴5x=5×15°=75°<90°,故本选项错误;
D、∵8k2+15k2=17k2,∴a2+b2=c2,故本选项正确.
故选C.
点评 本题考查的是勾股定理的逆定理及直角三角形的性质,若已知三角形的三边判定其形状时要根据勾股定理判断;若已知三角形各角之间的关系,应根据三角形内角和定理求出最大角的度数或求出两较小角的和再进行判断.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
15.已知a2=25,$\sqrt{{b}^{2}}$=7,且|a+b|=a+b,则a-b的值为( )
| A. | 2或12 | B. | 2或-12 | C. | -2或12 | D. | -2或-12 |
16.在下列实数中,无理数是( )
| A. | 0 | B. | -$\frac{22}{7}$ | C. | $\sqrt{2}$ | D. | $\sqrt{9}$ |
20.在实数:-$\sqrt{2}$,3.14159,$\root{3}{27}$,π,1.010010001…,4.$\stackrel{•}{2}$$\stackrel{•}{1}$,$\frac{1}{3}$中,无理数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
10.在平面直角坐标系中,点P的坐标为(3,-1),那么点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.下列一元二次方程有两个相等实数根的是( )
| A. | x2+4=0 | B. | x2-2x=0 | C. | (x+1)2=0 | D. | (x-3)(x+1)=0 |
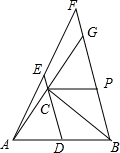 如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=$\frac{1}{3}$CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=$\frac{1}{3}$CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.