题目内容
10.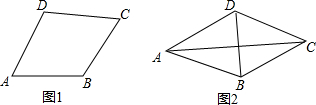 类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)如图1,在四边形ABCD中添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.
(2)问题探究
小红提出了一个猜想:对角线互相平分且相等的“等邻边四边形”是正方形.她的猜想正确吗?请说明理由.
(3)如图2,“等邻边四边形”ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,$AC=\sqrt{2}AB$.试探究线段BC,CD,BD之间的数量关系,并证明你的结论.
分析 (1)利用“等邻边四边形”的定义添加条件即可.
(2)用矩形和菱形的判定,先判断出四边形既是矩形,又是菱形,从而得到它是正方形;
(3)先判断出△ACF∽△ABD,得到$CF=\sqrt{2}BD$,再求出∠CBF=90°,最后用勾股定理即可求解.
解答 解:(1)AB=BC,
理由:∵四边形ABCD是凸四边形,且AB=BC,
∴四边形ABCD是“等邻边四边形”.
(2)①正确;理由为:
∵四边形的对角线互相平分且相等,
∴四边形ABCD是矩形
∵四边形是“等邻边四边形”,
∴这个四边形有一组邻边相等,
∴四边形ABCD是菱形
∴对角线互相平分且相等的等邻边四边形是正方形,
(3)BC2+CD2=2BD2
证明:如图,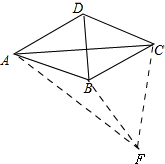
∵AB=AD,
∴将△ADC线绕点A旋转到△ABF,连接CF,则△ABF≌△ADC,
∴∠ABF=∠ADC,∠BAF=∠DAC,AF=AC,FB=CD,
∴∠BAD=∠CAF,$\frac{AC}{AD}=\frac{AF}{AB}$,
∴△ACF∽△ABD,
∴$\frac{CF}{BD}=\frac{AC}{AB}$,
∵$AC=\sqrt{2}AB$,
∴$CF=\sqrt{2}BD$,
∵∠BAD+∠ADC+∠BCD+∠ABC=360°,
∴∠ABC+∠ADC=360°-(∠BAD+∠BCD)=360°-90°=270°
∴∠ABC+∠ABF=270°,
∴∠CBF=90°,
∴$B{C^2}+F{B^2}=C{F^2}={({\sqrt{2}BD})^2}=2B{D^2}$
∴BC2+CD2=2BD2.
点评 此题是四边形综合题,主要考查了新定义的理解,矩形,菱形,正方形的性质和判定,勾股定理,三角形全等和相似的性质和判定,解本题的关键是作出辅助线分别判断出三角形相似和全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
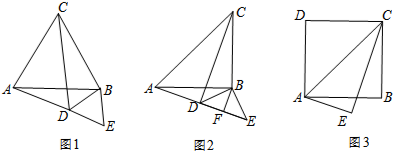
 如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.
如图,将△ABC沿BC折叠得到△BCD,再将△BCD沿BD折叠得到△BDE,设折叠后所得多边形的边数为n.