题目内容
7.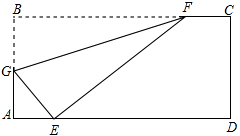 如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.
如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.(1)当BF的最小值等于6时,才能使点B落在AD上一点E处;
(2)当点F与点C重合时,求AE的长;
(3)当AE=3时,点F离点B有多远?
分析 (1)当点G与点A重合时,BF的值最小,即可求出BF的最小值等于6;
(2)在RT△CDE中运用勾股定理求出DE,再利用AE=AD-DE即可求出答案;
(3)作FH⊥AD于点H,设AG=x,利用勾股定理可先求出AG,可得EG,利用△AEG∽△HFE,由$\frac{EF}{EG}$=$\frac{FH}{AE}$可求出EF,即得出BF的值.
解答 解:(1)点G与点A重合时,如图1所示,四边形ABFE是正方形,此时BF的值最小,即BF=AB=6.当BF的最小值等于6时,才能使B点落在AD上一点E处;
故答案为:6.
(2)如图2所示,
∵在Rt△CDE中,CE=BC=10,CD=6,
∴DE=$\sqrt{C{E}^{2}-C{D}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AE=AD-DE=10-8=2,
(3)如图3所示,作FH⊥AD于点H,
AE=3,设AG=y,则BG=EG=6-y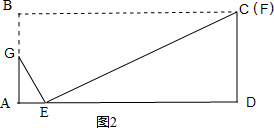 ,
,
根据勾股定理得:
(6-y)2=y2+9,
解得:y=$\frac{9}{4}$,
∴EG=BG=$\frac{15}{4}$,
又△AEG∽△HFE,
∴$\frac{EF}{EG}$=$\frac{FH}{AE}$,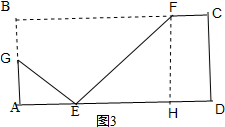
∴$\frac{EF}{\frac{15}{4}}=\frac{6}{3}$,
∴EF=$\frac{15}{2}$,
∴BF=EF=$\frac{15}{2}$.
点评 本题主要考查了翻折变换,解题的关键是折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
10.下列调查中,最适合用普查方式的是( )
| A. | 调查一批电视机的使用寿命情况 | |
| B. | 调查某中学九年级一班学生的视力情况 | |
| C. | 调查重庆市初中学生每天锻炼所用的时间情况 | |
| D. | 调查重庆市初中学生利用网络媒体自主学习的情况 |
15.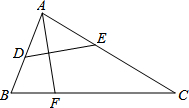 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
2.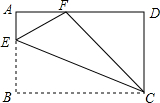 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
12. 如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
 如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )| A. | 30°或50° | B. | 30°或60° | C. | 40°或50° | D. | 40°或60° |
19.某服装经销商发现某款新型运动服市场需求量较大,经过市场调查发现年销售量y(件)与销售单价x(元)之间存在如图1所示的一次函数关系,而该服装的进价z(元)与销售量y(件)之间的关系如下表所示.已知每年支付员工工资和场地租金等费用总计2万元.
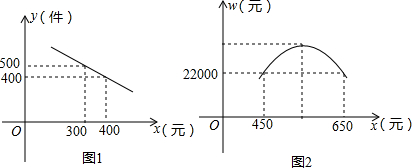
(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
| 销售数量y(件) | … | 300 | 400 | 500 | 600 | … |
| 进货价格z(元) | … | 340 | 320 | 300 | 280 | … |

(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
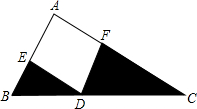 如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.
如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.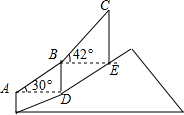 如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)