题目内容
15.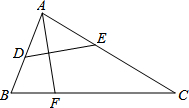 如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
分析 认真审题,可以发现,AC=CE+AE,若要使CE最大,只要使AE最小即可,连接EF,则:EF=AE,过只要EF最小即可,据此即可得解.
解答 解:如图,连接EF,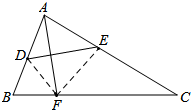
当EF⊥BC时,EF最短,即CE最长,
∵∠C=30°,
∴EF=$\frac{1}{2}$CE,
∵沿着DE对折,使点A落在BC边上的点F处,
∴EF=AE,
∴EF+CE=AC=8,即:$\frac{1}{2}CE+CE$=8,
解得:CE=$\frac{16}{3}$,
∴CE的最大值为$\frac{16}{3}$.
故选B.
点评 本题主要考查了垂线段最短,以及在翻折变换时,变换前后的线段和角度不变,还考查了解直角三角形的知识,有一定的综合性,要注意认真总结.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列计算正确的是( )
| A. | ab•ab=2ab | B. | (2a)3=2a3 | C. | 3$\sqrt{a}$-$\sqrt{a}$=3(a≥0) | D. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$(a≥0,b≥0) |
4.如图1,在等边△ABC中,点P以每秒1厘米的速度从点A出发,沿折线AB-BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )
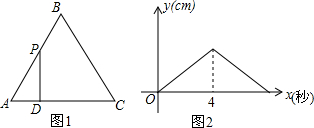

| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\frac{5\sqrt{3}}{4}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
 二次函数y=$\sqrt{3}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=$\sqrt{3}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为2$\sqrt{3}$.
二次函数y=$\sqrt{3}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=$\sqrt{3}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为2$\sqrt{3}$.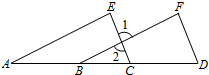 已知:如图,点A,B,C,D在同一直线上,∠F=∠E,DF∥EC.
已知:如图,点A,B,C,D在同一直线上,∠F=∠E,DF∥EC.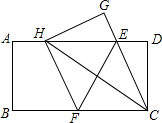 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②当CH=CB时,EC平分∠DCH;③当点H与点A重台时,BF=3;④当点H是AD中点时,EF=4$\sqrt{3}$,其中正确的结论有①②③(填写所有正确的序号).
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②当CH=CB时,EC平分∠DCH;③当点H与点A重台时,BF=3;④当点H是AD中点时,EF=4$\sqrt{3}$,其中正确的结论有①②③(填写所有正确的序号).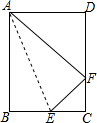 如图,纸片矩形ABCD中,已知:AB=10,AD=8.将AB沿AE折叠,使点B落在边CD的F处,试求:
如图,纸片矩形ABCD中,已知:AB=10,AD=8.将AB沿AE折叠,使点B落在边CD的F处,试求: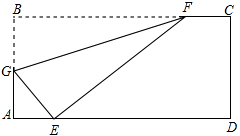 如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.
如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.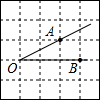 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=$\frac{1}{2}$.
如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=$\frac{1}{2}$.