题目内容
11.先化简:($\frac{x+1}{x-1}$+1)÷$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$+$\frac{2-2x}{{x}^{2}-1}$,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时根据除法法则变形,约分得到最简结果,将x=0代入计算即可求出值.
解答 解:($\frac{x+1}{x-1}$+1)÷$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$+$\frac{2-2x}{{x}^{2}-1}$
=$\frac{x+1+x-1}{x-1}•\frac{(x-1)^{2}}{x(x+1)}+\frac{2(1-x)}{(x+1)(x-1)}$
=$\frac{2x}{x-1}•\frac{(x-1)^{2}}{x(x+1)}-\frac{2}{x+1}$
=$\frac{2x-4}{x+1}$
满足-2≤x≤2的整数有:-2、-1、0、1、2
但x=-1、0、1时,原式无意义,
∴x=-2或2
∴当x=2时,原式=0.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
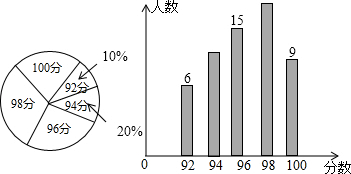

| A. | 94分,96分 | B. | 96分,96分 | C. | 94分,96.4分 | D. | 96分,96.4分 |
 二次函数y=$\sqrt{3}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=$\sqrt{3}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为2$\sqrt{3}$.
二次函数y=$\sqrt{3}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=$\sqrt{3}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为2$\sqrt{3}$.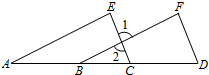 已知:如图,点A,B,C,D在同一直线上,∠F=∠E,DF∥EC.
已知:如图,点A,B,C,D在同一直线上,∠F=∠E,DF∥EC.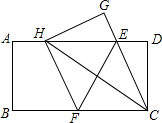 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②当CH=CB时,EC平分∠DCH;③当点H与点A重台时,BF=3;④当点H是AD中点时,EF=4$\sqrt{3}$,其中正确的结论有①②③(填写所有正确的序号).
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②当CH=CB时,EC平分∠DCH;③当点H与点A重台时,BF=3;④当点H是AD中点时,EF=4$\sqrt{3}$,其中正确的结论有①②③(填写所有正确的序号).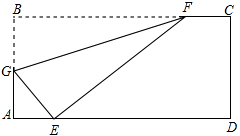 如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.
如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.