题目内容
2.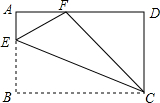 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
分析 如图,首先运用勾股定理求出DF的长度,进而求出AF的长度;其次运用翻折变换的性质证明EF=BE(设为λ),进而得到AE=4-λ,此为解题的关键性结论;运用勾股定理列出关于λ的方程,求出λ即可解决问题.
解答 解:如图, 由题意得:
由题意得:
CD=AB=4,AD=BC=5,
CF=BC=5,∠A=∠D=90°;
由勾股定理得:
DF2=CF2-CD2,
∴DF=3,AF=5-3=2;
由翻折变换的性质得:
EF=BE(设为λ),则AE=4-λ,
由勾股定理得:λ2=22+(4-λ)2,
解得:$λ=\frac{5}{2}$,AE=4-$\frac{5}{2}$=$\frac{3}{2}$,
∴tan∠AFE=$\frac{AE}{AF}$=$\frac{3}{4}$,
故选:A.
点评 该题以矩形为载体,以翻折变换为手段,以考查矩形的性质、勾股定理等几何知识点为核心构造而成;牢固掌握矩形的性质、勾股定理等几何知识点是基础,灵活运用、解题是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
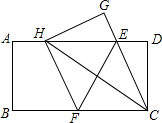 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②当CH=CB时,EC平分∠DCH;③当点H与点A重台时,BF=3;④当点H是AD中点时,EF=4$\sqrt{3}$,其中正确的结论有①②③(填写所有正确的序号).
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②当CH=CB时,EC平分∠DCH;③当点H与点A重台时,BF=3;④当点H是AD中点时,EF=4$\sqrt{3}$,其中正确的结论有①②③(填写所有正确的序号).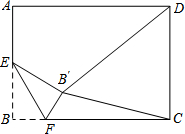 如图所示,在矩形ABC中,AB=4,AD=4$\sqrt{2}$,E是线段AB的中点,F是线段BC上的动点,△BEF沿直线EF翻折到△B′EF,连结DB′,B′C.当DB′最短时,则sin∠B′CF=$\frac{\sqrt{3}}{3}$.
如图所示,在矩形ABC中,AB=4,AD=4$\sqrt{2}$,E是线段AB的中点,F是线段BC上的动点,△BEF沿直线EF翻折到△B′EF,连结DB′,B′C.当DB′最短时,则sin∠B′CF=$\frac{\sqrt{3}}{3}$.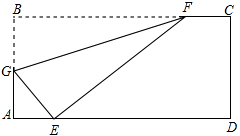 如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.
如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.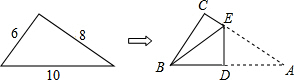 如图,一个三角形三边长为6,8,10,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长是$\frac{7}{4}$.
如图,一个三角形三边长为6,8,10,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长是$\frac{7}{4}$.