题目内容
17.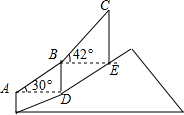 如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
分析 要求缆车从点A运行到点C的垂直上升的距离,就是求BD+CE的值.解直角△ADB,利用30°角所对的直角边等于斜边的一半得出BD=$\frac{1}{2}$AB=100m,解直角△CEB,根据正弦函数的定义可得CE=BC•sin42°.
解答 解:在直角△ADB中,∵∠ADB=90°,∠BAD=30°,AB=200m,
∴BD=$\frac{1}{2}$AB=100m,
在直角△CEB中,∵∠CEB=90°,∠CBE=42°,CB=200m,
∴CE=BC•sin42°≈200×0.67=134m,
∴BD+CE≈100+134=234m.
答:缆车从点A运行到点C的垂直上升的距离约为234m.
点评 本题考查了解直角三角形的应用-坡度坡角问题,锐角三角函数的定义,结合图形理解题意是解决问题的关键.

练习册系列答案
相关题目
8.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
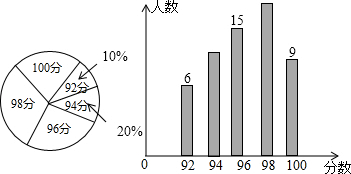

| A. | 94分,96分 | B. | 96分,96分 | C. | 94分,96.4分 | D. | 96分,96.4分 |
6.下列运算正确的是( )
| A. | a•a3=a3 | B. | 2(a-b)=2a-b | C. | (a3)2=a5 | D. | a2-2a2=-a2 |
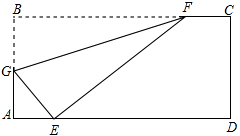 如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.
如图,折叠矩形纸片ABCD,使点B落在AD边上一点E处,折痕的两端点分别在边AB,BC上(含端点),且AB=6,BC=10,设AE=x.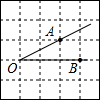 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=$\frac{1}{2}$.
如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=$\frac{1}{2}$.
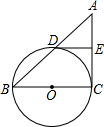 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.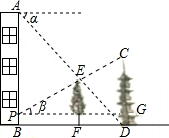 如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)
如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)