题目内容
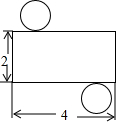 观察图中的图形:
观察图中的图形:(1)由该图形可以围成一个什么样的立体图形?
(2)画出你围成的立体图形的三视图.
(3)计算你围成的立体图形的体积.
考点:由三视图判断几何体
专题:
分析:(1)从几何体的展开图和圆柱的特征即可作出判断;
(2)根据圆柱的特征可以得到正视图以及左视图为矩形,而俯视图为圆形;
(3)先得到圆柱的半径和高,再根据圆柱的体积公式即可求解.
(2)根据圆柱的特征可以得到正视图以及左视图为矩形,而俯视图为圆形;
(3)先得到圆柱的半径和高,再根据圆柱的体积公式即可求解.
解答:解:(1)由该图形可以围成一个圆柱的立体图形;
(2)如图所示:

(3)围成的立体图形的体积:
π×(
)2×2=
.
答:围成的立体图形的体积是
.
(2)如图所示:

(3)围成的立体图形的体积:
π×(
| 4 |
| 2π |
| 8 |
| π |
答:围成的立体图形的体积是
| 8 |
| π |
点评:考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查;圆柱体积公式:圆柱体积=底面积×高.

练习册系列答案
相关题目
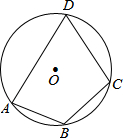 如图,圆上有A、B、C、D四点,其中∠BCD=100°,若
如图,圆上有A、B、C、D四点,其中∠BCD=100°,若 |
| ABC |
 |
| ADC |
 |
| BAD |
| A、15π | B、10π |
| C、8π | D、4π |
若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
| A、1个或2个或3个 |
| B、0个或1个或2个或3个 |
| C、1个或2个 |
| D、以上都不对 |
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的.若BF=AC,∠ABC=40°,则∠CAC′=
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的.若BF=AC,∠ABC=40°,则∠CAC′=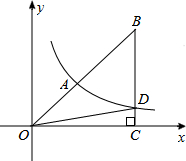 如图,双曲线y=
如图,双曲线y=