题目内容
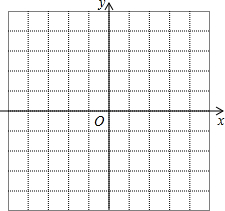
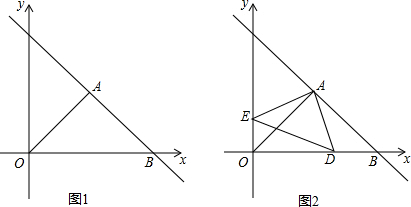
如图,在△ABO中,已知AB=AO,∠BAO=90°,BO=8cm,以点O为原点,BO所在的直线为x轴建立平面直角坐标系,
(1)求点A的坐标及直线AB的解析式;
(2)动点D从点O出发沿x轴的正半轴以每秒2cm的速度运动,动点E也同时从点O沿y轴正半轴以每秒1cm的速度运动,连接AD、AE、DE,设运动时间为t秒,当t为何值时,△ADE是以AE为腰的等腰三角形?
(3)在(2)的条件下,直线AB上是否存在点F,使得△AEF和△ABD的面积相等?若存在,请直接写出F点的坐标;若不存在,请说明理由.
(1)求点A的坐标及直线AB的解析式;
(2)动点D从点O出发沿x轴的正半轴以每秒2cm的速度运动,动点E也同时从点O沿y轴正半轴以每秒1cm的速度运动,连接AD、AE、DE,设运动时间为t秒,当t为何值时,△ADE是以AE为腰的等腰三角形?
(3)在(2)的条件下,直线AB上是否存在点F,使得△AEF和△ABD的面积相等?若存在,请直接写出F点的坐标;若不存在,请说明理由.

考点:一次函数综合题
专题:
分析:(1)根据等腰直角三角形的性质,可得A点坐标,根据待定系数法,可得AB的函数解析式;
(2)根据运动速度乘以运动时间,可得E、D点坐标,革命剧AE=AD,AE=ED,可得关于t的方程,根据解方程,可得t值;
(3)根据点到直线的距离,可得E到AF的距离,根据三角形的面积相等,可得关于相等的多项式,根据相等的多项式一次项的系数相等,常数项相等,可得关于a的值,可得答案.
(2)根据运动速度乘以运动时间,可得E、D点坐标,革命剧AE=AD,AE=ED,可得关于t的方程,根据解方程,可得t值;
(3)根据点到直线的距离,可得E到AF的距离,根据三角形的面积相等,可得关于相等的多项式,根据相等的多项式一次项的系数相等,常数项相等,可得关于a的值,可得答案.
解答:解:(1)如图,作AD⊥OB与D点,

由AB=AO,∠BAO=90°,得△AOB是等腰直角三角形.
OD=BD=AD=4(cm).即A(4,4).
设直线AB的解析式是y=kx+b,图象过点A、B,得
.解得
,
直线AB的解析式是y=-x+8;
(2)由动点D从点O出发沿x轴的正半轴以每秒2cm的速度运动,动点E也同时从点O沿y轴正半轴以每秒1cm的速度运动,
E(0,t),D(2t,0).
当AE=AD时,AE2=AD2,即(t-4)2+42=(2t-4)2+42,解得t=
,t=0(不符合题意的要舍去),
当AE=ED时,AE2=ED2,即(t-4)2+42=t2+(2t)2,解得t=-4(不符合题意的要舍去),t=2,
综上所述:t=2,t=
,△ADE是以AE为腰的等腰三角形;
(3)如图2:作EG⊥AF于G点,作AH⊥DB于点H,

设F点坐标(a,8-a),E(0,t),D(2t,0).
DB=8-2t,AF=
=(a-4)
.
点到AF的长,EG=
.
由△AEF和△ABD的面积相等,得
AF•EG=
DB•AH,即
(a-4)
=
×4(8-2t)
当t<4时,
(a-4)×8-
(a-4)t=16-4t,解得a=8即F1(8,0);
当4<t<8时.
(a-4)×8-
(a-4)t=4t-16,解得a=-4即F2(-4,12);
当t>8时,-
(a-4)×8+
(a-4)t=4t-16,解得a=12,即F3(12,-4);
综上所述:F1(8,0),F2(-4,12),F3(12,-4)时,△AEF和△ABD的面积相等.

由AB=AO,∠BAO=90°,得△AOB是等腰直角三角形.
OD=BD=AD=4(cm).即A(4,4).
设直线AB的解析式是y=kx+b,图象过点A、B,得
|
|
直线AB的解析式是y=-x+8;
(2)由动点D从点O出发沿x轴的正半轴以每秒2cm的速度运动,动点E也同时从点O沿y轴正半轴以每秒1cm的速度运动,
E(0,t),D(2t,0).
当AE=AD时,AE2=AD2,即(t-4)2+42=(2t-4)2+42,解得t=
| 8 |
| 3 |
当AE=ED时,AE2=ED2,即(t-4)2+42=t2+(2t)2,解得t=-4(不符合题意的要舍去),t=2,
综上所述:t=2,t=
| 8 |
| 3 |
(3)如图2:作EG⊥AF于G点,作AH⊥DB于点H,

设F点坐标(a,8-a),E(0,t),D(2t,0).
DB=8-2t,AF=
| (a-4)2+(8-a-4)2 |
| 2 |
点到AF的长,EG=
| |t-8| | ||
|
由△AEF和△ABD的面积相等,得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| |t-8| | ||
|
| 1 |
| 2 |
当t<4时,
| 1 |
| 2 |
| 1 |
| 2 |
当4<t<8时.
| 1 |
| 2 |
| 1 |
| 2 |
当t>8时,-
| 1 |
| 2 |
| 1 |
| 2 |
综上所述:F1(8,0),F2(-4,12),F3(12,-4)时,△AEF和△ABD的面积相等.
点评:本题考查了一次函数综合题,(1)利用了等腰直角三角形的性质,待定系数法求解析式,(2)利用了等腰三角形的定义,分类讨论是解题关键;(3)利用了三角形的面积公式,分了讨论是解题关键.

练习册系列答案
相关题目
 观察图中的图形:
观察图中的图形: 如图,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB,求∠EOB的度数.
如图,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB,求∠EOB的度数.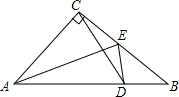 如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证:
如图,已知在△ABC中,∠ACB=90°,AC=BC,AE是角平分线,ED⊥AB,垂足为D.求证: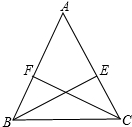 已知在△ABC中,AB=AC,CF⊥AB于F,BE⊥AC于E,求证:AE=AF.
已知在△ABC中,AB=AC,CF⊥AB于F,BE⊥AC于E,求证:AE=AF.