题目内容
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的.若BF=AC,∠ABC=40°,则∠CAC′=
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的.若BF=AC,∠ABC=40°,则∠CAC′=考点:旋转的性质
专题:计算题
分析:先根据旋转的性质得AC=AC′,AB=AB′,∠CAC′=∠BAB′,根据等腰三角形的性质和三角形内角和定理得到∠1=∠3=
(180°-∠CAC′),∠2=
(180°-∠BAB′),则∠1=∠2,再利用“AAS”证明△BEF≌△CEA,得到EB=EC,所以∠ECB=∠EBC=40°,则利用互余可计算出∠1=50°,然后根据三角形内角和可计算出∠CAC′.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
解:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC′,AB=AB′,∠CAC′=∠BAB′,
∴∠1=∠3=
(180°-∠CAC′),∠2=
(180°-∠BAB′),
∴∠1=∠2,
在△BEF和△CEA中,
,
∴△BEF≌△CEA(AAS),
∴EB=EC,
∴∠ECB=∠EBC=40°,
∴∠1=90°-∠ECB=50°,
∴∠CAC′=180°-2∠1=100°.
故答案为100°.
 解:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
解:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,∴AC=AC′,AB=AB′,∠CAC′=∠BAB′,
∴∠1=∠3=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
在△BEF和△CEA中,
|
∴△BEF≌△CEA(AAS),
∴EB=EC,
∴∠ECB=∠EBC=40°,
∴∠1=90°-∠ECB=50°,
∴∠CAC′=180°-2∠1=100°.
故答案为100°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
已知x1=-1,x2=2是方程x2+mx+n=0的两根,则m的值是( )
| A、1 | B、-1 | C、2 | D、-1 |
 为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表. 观察图中的图形:
观察图中的图形: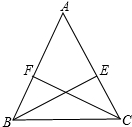 已知在△ABC中,AB=AC,CF⊥AB于F,BE⊥AC于E,求证:AE=AF.
已知在△ABC中,AB=AC,CF⊥AB于F,BE⊥AC于E,求证:AE=AF.