题目内容
16.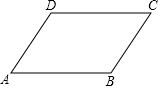 如图,在?ABCD中,下列等式成立的是( )
如图,在?ABCD中,下列等式成立的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |
分析 根据平行四边形法则逐一判断可得.
解答 解:如图,
∵四边形ABCD是平行四边形,
∴AB∥CD、AD∥BC,且AB=CD、AD=BC,
∴$\overrightarrow{AB}$+$\overrightarrow{CD}$=0,而$\overrightarrow{AD}$+$\overrightarrow{BD}$≠0,故A选项错误;
∵$\overrightarrow{AC}$≠$\overrightarrow{BD}$,
∴$\overrightarrow{AC}$-$\overrightarrow{BD}$≠0,故B选项错误;
由图可知,$\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AE}$,
$\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{CF}$-$\overrightarrow{CA}$=$\overrightarrow{AF}$,
∵$\overrightarrow{AE}$≠$\overrightarrow{AF}$,
∴$\overrightarrow{AB}$-$\overrightarrow{CD}$≠$\overrightarrow{AC}$+$\overrightarrow{BD}$,故C选项错误;
∵$\overrightarrow{AC}$-$\overrightarrow{BD}$=-$\overrightarrow{CA}$+$\overrightarrow{CE}$=$\overrightarrow{AE}$,
∴$\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$,故D选项正确.
点评 本题主要考查平行四边形的性质和平面向量的运算,熟练掌握平面向量的平行四边形法则是解题的关键.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案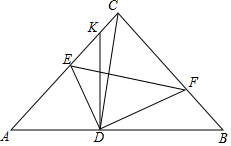 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.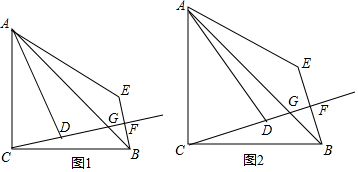
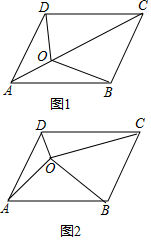 我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形.
我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形. 如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片②即可.
如图,一块三角形玻璃裂成①②两块,现需配一块同样的玻璃,为方便起见,只需带上碎片②即可.