题目内容
6.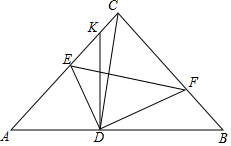 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.(1)求证:△DEK∽△DFB.
(2)当点K在线段AC上时,若CD=$\sqrt{10}$时,试求AK的长.
(3)若点K为EC中点时,试求AD的值.
分析 (1)根据等腰直角三角形的性质、翻转变换的性质证明∠EKD=∠FBD,∠EDK=∠FDB即可;
(2)作CH⊥AB于H,根据直角三角形的性质求出AH、BH、CH,根据相似三角形的性质列出比例式,计算即可;
(3)根据△DEK∽△DFB、等腰直角三角形的性质列出比例式,计算即可.
解答 (1)证明:由折叠可得:∠EDF=∠ACB=90°,∠DFE=∠CFE.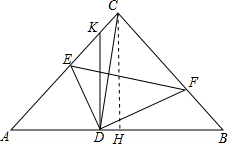
∵△ABC是等腰直角三角形,∠C=90°,
∴∠A=∠B=45°.
∵DK⊥AB,
∴∠ADK=∠BDK=90°,
∴∠AKD=45°,∠EDF=∠KDB=90°,
∴∠EKD=∠FBD,∠EDK=∠FDB,
∴△DEK∽△DFB;
(2)解:作CH⊥AB于H,
∵△ABC是等腰直角三角形,∠C=90°,
∴CH=AH=BH=$\frac{1}{2}$AB=3,
∴DH=$\sqrt{C{D}^{2}-C{H}^{2}}$=1,
∴AD=AH-DH=2,
∵△ABC是等腰直角三角形,AB=6,
∴AC=3$\sqrt{2}$,
∵DK⊥AB,CH⊥AB,
∴DK∥CH,
∴$\frac{AK}{AC}$=$\frac{AD}{AH}$,即$\frac{AK}{3\sqrt{2}}$=$\frac{2}{3}$,
解得,AK=2$\sqrt{2}$;
(3)解:∵△DEK∽△DFB,
∴$\frac{DK}{BD}$=$\frac{EK}{BF}$,
∵K为EC中点,
∴$\frac{BF}{DF}$=$\frac{EK}{ED}$=$\frac{1}{2}$,
∴BF=$\sqrt{2}$,
设AD=DK=x,
则AK=$\sqrt{2}$x,CK=EK=3$\sqrt{2}$-$\sqrt{2}$x,BD=6-x,
∴$\frac{3\sqrt{2}-\sqrt{2}x}{\sqrt{2}}$=$\frac{x}{6-x}$,
解得,x1=5-$\sqrt{7}$,x2=5+$\sqrt{7}$(舍去),
答:AD的值为5+$\sqrt{7}$.
点评 本题考查的是相似三角形的判定和性质、等腰直角三角形的性质、翻转变换的性质,掌握相似三角形的判定定理和性质定理是解题的关键.

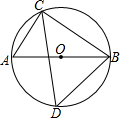 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )| A. | CD=(AC+BC)sinθ | B. | CD=(AC+BC)cosθ | ||
| C. | CD=AC•cosθ+BC•sinθ | D. | CD=AC•sinθ+BC•cosθ |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
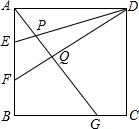 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
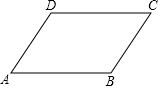 如图,在?ABCD中,下列等式成立的是( )
如图,在?ABCD中,下列等式成立的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |
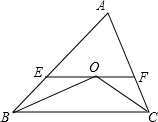 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.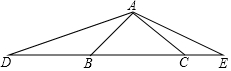 D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°.求证:CD2+BE2=DE2.
D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°.求证:CD2+BE2=DE2.