题目内容
7.若n满足(n-2017)2+(2018-n)2=1,求(2018-n)(n-2017)的值.分析 根据完全平方公式将[(n-2017)+(2018-n)]2展开后代入相关式子的即可求出答案.
解答 解:1=[(n-2017)+(2018-n)]2=(n-2017)2+(2018-n)2+2(n-2017)(2018-n)
∴1=1+2(n-2017)(2018-n)
∴(2018-n)(n-2017)=0,
点评 本题考查完全平方公式,解题的关键是利用整体的思想将[(n-2017)+(2018-n)]2展开,本题属于中等题型.

练习册系列答案
相关题目
18.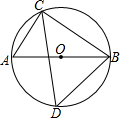 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )| A. | CD=(AC+BC)sinθ | B. | CD=(AC+BC)cosθ | ||
| C. | CD=AC•cosθ+BC•sinθ | D. | CD=AC•sinθ+BC•cosθ |
15.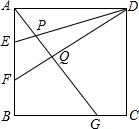 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
19.我们已经学习了利用配方法解一元二次方程,其实配方法还有其它重要应用.
例:已知x可取任何实数,试求二次三项式2x2-12x+14的值的范围.
解:2x2-12x+14=2(x2-6x)+14=2(x2-6x+32-32)+14
=2[(x-3)2-9]+14=2(x-3)2-18+14=2(x-3)2-4.
∵无论x取何实数,总有(x-3)2≥0,∴2(x-3)2-4≥-4.
即无论x取何实数,2x2-12x+14的值总是不小于-4的实数.
问题:已知x可取任何实数,则二次三项式-3x2+12x+11的最值情况是( )
例:已知x可取任何实数,试求二次三项式2x2-12x+14的值的范围.
解:2x2-12x+14=2(x2-6x)+14=2(x2-6x+32-32)+14
=2[(x-3)2-9]+14=2(x-3)2-18+14=2(x-3)2-4.
∵无论x取何实数,总有(x-3)2≥0,∴2(x-3)2-4≥-4.
即无论x取何实数,2x2-12x+14的值总是不小于-4的实数.
问题:已知x可取任何实数,则二次三项式-3x2+12x+11的最值情况是( )
| A. | 有最大值-23 | B. | 有最小值-23 | C. | 有最大值23 | D. | 有最小值23 |
16.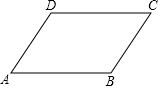 如图,在?ABCD中,下列等式成立的是( )
如图,在?ABCD中,下列等式成立的是( )
 如图,在?ABCD中,下列等式成立的是( )
如图,在?ABCD中,下列等式成立的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |
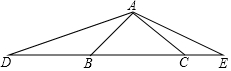 D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°.求证:CD2+BE2=DE2.
D、E是等腰Rt△ABC斜边BC所在直线上的两点,满足∠DAE=135°.求证:CD2+BE2=DE2. 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).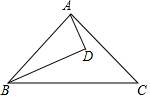 如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=15°,则∠BAD=35°.
如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=15°,则∠BAD=35°.