题目内容
1．
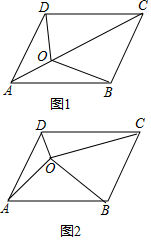
我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形．（1）若点O为平行四边形对角线AC上任意一点（不包括A、C）．如图1，上述结论是否还成立？若成立，说明理由；若不成立，说出它们之间还存在什么关系？为什么？
（2）若点O为平行四边形内任意一点，如图2，这四个小三角形又有怎样的关系？请直接写出结论，不需证明．
分析 （1）首先连接BD，交AC于点E，由四边形ABCD是平行四边形，可得BE=DE，然后由三角形中线的性质，证得S△ABE=S△ADE，S△OBE=S△ODE，S△BCE=S△DCE，继而求得答案．
（2）过O作EF⊥AD，交AD于E，交CD于F，由三角形面积公式得出S△AOD=$\frac{1}{2}$AD•OE，S△BOC=$\frac{1}{2}$BC•OF，由平行四边形的性质得出∴S△AOD+S△BOC=$\frac{1}{2}$BC•EF=$\frac{1}{2}$四边形ABCD的面积，同理：S△AOB+S△COD=$\frac{1}{2}$平行四边形ABCD的面积，即可得出结论．
解答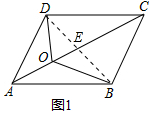 
解：（1）不成立．S△OAB=S△OAD，S△BOC=S△DOC．理由如下：
连接BD，交AC于点E，
∵四边形ABCD是平行四边形，
∴BE=DE，
∴S△ABE=S△ADE，S△OBE=S△ODE，S△BCE=S△DCE，
∴S△OAB=S△OAD，S△BOC=S△DOC．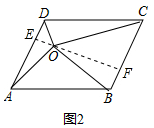
（2）S△AOD+S△BOC=S△AOB+S△COD．理由如下：
过O作EF⊥AD，交AD于E，交CD于F，如图2所示：
则S△AOD=$\frac{1}{2}$AD•OE，S△BOC=$\frac{1}{2}$BC•OF，
∴S△AOD+S△BOC=$\frac{1}{2}$BC•（OE+OF）=$\frac{1}{2}$BC•EF=$\frac{1}{2}$四边形ABCD的面积，
同理：S△AOB+S△COD=$\frac{1}{2}$平行四边形ABCD的面积，
∴S△AOD+S△BOC=S△AOB+S△COD．
点评 此题考查了平行四边形的性质以及三角形面积公式．熟练掌握平行四边形的性质和三角形面积公式，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
名校课堂系列答案
如图，直线l1：y=x+1与直线l2：y=mx+n相交于点P（1，b）．
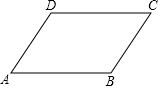如图，在?ABCD中，下列等式成立的是（ ）| A． | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B． | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C． | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D． | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |
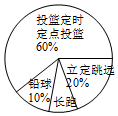某班同学响应“阳光体育运动”号召，利用课外活动积极参加体育锻炼，每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练，训练后都进行了测训练后篮球定点投篮测试进行球赛进球统计表| 进球数（个） | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
（1）训练后篮球定时定点投篮人均进球数为多少个？
（2）选择长跑训练的人数占全班人数的百分比是10%，该班共有同学40人；
（3）根据测试资料，参加蓝球定时定点投篮的学生训练后比训练前的人均进球增加了25%，求参加训练之前的人均进球数．