题目内容
5.高空的气温与距地面的高度有关,某地地面气温为24℃,且已知离地面距离每升高1 km,气温下降6℃.(1)写出该地空中气温T(℃)与高度h(km)之间的函数表达式;
(2)求距地面3 km处的气温T;
(3)求气温为-6℃处距地面的高度h.
分析 (1)直接利用空中气温T=地面温度-6×上升高度,进而得出答案;
(2)利用h=3,进而代入函数关系式求出答案;
(3)利用T=-6,进而代入函数关系式求出答案.
解答 解:(1)∵离地面距离每升高1 km,气温下降6℃,
∴该地空中气温T(℃)与高度h(km)之间的函数表达式为:T=24-6h;
(2)当h=3时,T=24-6×3=6(℃);
(3)当T=-6℃时,-6=24-6h,
解得:h=5,
答:距地面的高度h为5km.
点评 此题主要考查了函数关系式以及代数式求值,正确得出T与h的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.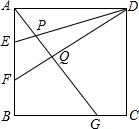 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P和Q,以下说法中正确的是( )①AG⊥FD;②AQ:QG=6:7;③EP:PD=2:11;④SGCDQ:SBGQF=17:9.
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①②④ |
16.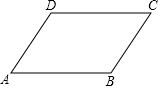 如图,在?ABCD中,下列等式成立的是( )
如图,在?ABCD中,下列等式成立的是( )
 如图,在?ABCD中,下列等式成立的是( )
如图,在?ABCD中,下列等式成立的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$+$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ | C. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{CD}$=$\overrightarrow{AC}$-$\overrightarrow{BD}$ |

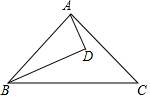 如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=15°,则∠BAD=35°.
如图,BD是∠ABC的角平分线,AD⊥BD,垂足为D,∠DAC=20°,∠C=15°,则∠BAD=35°.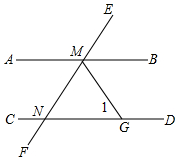 如图,AB∥CD,EF分别交AB,CD于M,N,∠END=50°,∠BMF的角平分线MG交CD于点G,求∠1的度数.
如图,AB∥CD,EF分别交AB,CD于M,N,∠END=50°,∠BMF的角平分线MG交CD于点G,求∠1的度数.