题目内容
20.李华晚上在两根相距40m的路灯杆下来回散步,已知李华身高AB=1.6m,灯柱CD=EF=8m.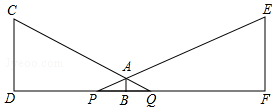
(1)若李华距灯柱CD的距离DB=16m,求他的影子BQ的长.
(2)若李华的影子PB=5m,求李华距灯柱CD的距离.
分析 (1)根据相似三角形的性质即可得到结论;
(2)根据相似三角形的性质和线段的和差即可得到.
解答 解:(1)∵AB∥CD,
∴△ABQ∽△CDQ,
∴$\frac{AB}{CD}$=$\frac{BQ}{DQ}$,即$\frac{1.6}{8}=\frac{BQ}{16+BQ}$,
∴BQ=4m;
(2)∵AB∥EF,
∴△ABP∽△EPF,
∴$\frac{AB}{EF}=\frac{PB}{PF}$,即$\frac{1.6}{8}=\frac{5}{PF}$,
∴PF=25,
∵DF=40,
∴BD=20m.
∴李华距灯柱CD的距离是20m.
点评 本题考查了相似三角形的应用,熟练掌握相似三角形的性质是解题的关键.

练习册系列答案
相关题目
10.某人去水果批发市场采购苹果,他看中了A、B两家苹果、这两家苹果品质一样,零售价都为10元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的90%优惠;批发数量不超过200千克,按零售价的80%优惠;超过200千克的按零售价的70%优惠.
B家的规定如表:
(1)如果他批发60千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(150<x<200),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发180千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的90%优惠;批发数量不超过200千克,按零售价的80%优惠;超过200千克的按零售价的70%优惠.
B家的规定如表:
| 数量范围(千克) | 0~50 | 50以上~150的部分 | 150以上~250的部分 | 250以上的部分 |
| 价格(元) | 零售价的90% | 零售价的80% | 零售价的70% | 零售价的60% |
(2)如果他批发x千克苹果(150<x<200),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发180千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
5.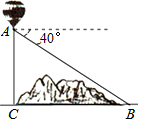 如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )
如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )
 如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )
如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升a米处,在A处观察B地的俯角为40°,则BC两地之间的距离为( )| A. | asin40°米 | B. | acos40°米 | C. | atan40°米 | D. | $\frac{a}{tan40°}$米 |
9.用配方法解方程x2-2x-8=0,下列配方结果正确的是( )
| A. | (x+1)2=9 | B. | (x+1)2=7 | C. | (x-1)2=9 | D. | (x-1)2=7 |
 如图,将△ABC绕点B逆时针旋转60°得到△A′C′B,且BC=2,那么CC′的长是2.
如图,将△ABC绕点B逆时针旋转60°得到△A′C′B,且BC=2,那么CC′的长是2.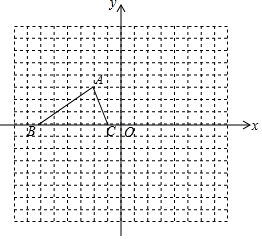 如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).