题目内容
9．
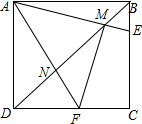已知正方形ABCD是一个正方形，E是BC上一点，F是CD上一点，∠EAF=45°，AE、AF分别交BD于M、N，连接MF，求证：AM⊥MF，AM=MF．
分析 由正方形的性质得出∠ADF=90°，∠ADM=∠FDM=45°，再由已知条件得出∠FDM=∠EAF，证出A、D、F、E四点共圆，由圆周角定理得出AF是直径，$\widehat{AM}÷\widehat{FM}$，得出∠AMF=90°，AM=MF，即可得出AM⊥MF．
解答 证明：∵四边形ABCD是正方形，
∴∠ADF=90°，∠ADM=∠FDM=45°，
∵∠EAF=45°，
∴∠FDM=∠EAF，
∴A、D、F、E四点共圆，
∵∠ADF=90°，∠ADM=∠FDM，
∴AF是直径，$\widehat{AM}÷\widehat{FM}$，
∴∠AMF=90°，AM=MF，
∴AM⊥MF．
点评 本题考查了正方形的性质、四点共圆、圆周角定理、圆心角、弧、弦之间的关系定理；熟练掌握正方形的性质，证明四点共圆是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：
（1）该二次函数图象与y轴的交点坐标是（0，3）；顶点坐标是（2，-1）；函数表达式是y=x2-4x+3．
（2）若点（x1，y1）、（x2，y2）都在该函数图象上，当x1＜x2＜2时，则y1＞y2（填“＜”“＞”或“=”号）．
| x | … | -1 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 0 | -1 | 0 | 3 | … |
（2）若点（x1，y1）、（x2，y2）都在该函数图象上，当x1＜x2＜2时，则y1＞y2（填“＜”“＞”或“=”号）．
1．已知点P（a+1，2a-3）关于x轴的对称点在第二象限，则a的取值范围是（ ）
| A． | -1＜a＜$\frac{3}{2}$ | B． | -$\frac{3}{2}$＜a＜1 | C． | a＜-1 | D． | a$＞\frac{3}{2}$ |
