题目内容
20.已知:$\frac{y}{x}$+$\frac{x}{y}$=a,$\frac{y}{x}$-$\frac{x}{y}$=b,则a2-b2=4.分析 先把要求的式子进行因式分解,然后把已知算式代入,根据分式的混合运算法则计算即可.
解答 解:a2-b2=(a+b)(a-b)
=($\frac{y}{x}$+$\frac{x}{y}$+$\frac{y}{x}$-$\frac{x}{y}$)($\frac{y}{x}$+$\frac{x}{y}$-$\frac{y}{x}$+$\frac{x}{y}$)
=$\frac{2y}{x}$•$\frac{2x}{y}$
=4,
故答案为:4.
点评 本题主要考查分式的混合运算,掌握平方差公式、通分和约分的法则以及因式分解是解答的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
8.下列说法正确的是( )
| A. | 两条射线组成的图形叫做角 | |
| B. | 角的大小与角的两边张开的程度有关 | |
| C. | 角的两边越长,角越大 | |
| D. | 任何一个角都可以用角的顶点字母来表示 |
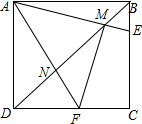 已知正方形ABCD是一个正方形,E是BC上一点,F是CD上一点,∠EAF=45°,AE、AF分别交BD于M、N,连接MF,求证:AM⊥MF,AM=MF.
已知正方形ABCD是一个正方形,E是BC上一点,F是CD上一点,∠EAF=45°,AE、AF分别交BD于M、N,连接MF,求证:AM⊥MF,AM=MF.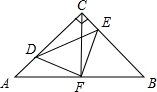 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.