题目内容
18．因式分解：（1）-2（m-n）2+32；
（2）（x+2）（x+4）+x2-4．
分析 （1）根据提公因式法，可得平方差公式，根据平方差公式，可得答案；
（2）根据平方差公式，可得公因式，根据提公因式法，可得答案．
解答 解：（1）原式=-2[（m-n）2-16]=-2[（m-n+4）（m-n-4）]=-2（m-n+4）（m-n-4）；
（2）原式=（x+2）（x+4）+（x+2）（x-2）
=（x+2）[（x+4）+（x-2）]
=（x+2）（2x+2）
=2（x+2）（x+1）．
点评 本题考查了因式分解，利用平方差公式得出公因式是解题关键，注意分解要彻底．
练习册系列答案
相关题目
8．下列说法正确的是（ ）
| A． | 两条射线组成的图形叫做角 | |
| B． | 角的大小与角的两边张开的程度有关 | |
| C． | 角的两边越长，角越大 | |
| D． | 任何一个角都可以用角的顶点字母来表示 |
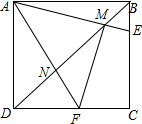已知正方形ABCD是一个正方形，E是BC上一点，F是CD上一点，∠EAF=45°，AE、AF分别交BD于M、N，连接MF，求证：AM⊥MF，AM=MF．
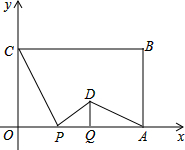如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA=8，OC=4．点P从点O出发，沿x轴以每秒2个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D，点D随点P的运动而运动，连接DP、DA，过点D作DQ⊥OA，交OA于点Q．
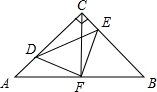如图，在等腰Rt△ABC中，∠ACB=90°，AC=CB，F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD=CE．连接DE、DF、EF．