题目内容
19.如图,在平行四边形OABC中,点A在x轴上,∠AOC=60°,OC=4cm,OA=8cm,动点P从点O出发,以1cm/s的速度沿线段OA-AB运动;动点Q同时从点O出发,以1cm/s的速度沿线段OC-CB运动,其中一点先到达终点B时,另一点也随之停止运动,设运动时间为t秒.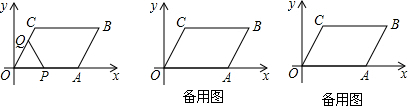
(1)填空:点C的坐标是(2,2$\sqrt{3}$),对角线OB的长度是4$\sqrt{7}$cm;
(2)设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
分析 (1)作CE⊥OA于E,根据锐角三角函数的概念求出OE、CE的长,求出点C的坐标,根据勾股定理求出BD的长;
(2)分当0<t≤4时,当4≤t≤8时,当8≤t<12时三种情况,根据三角形面积公式计算即可.
解答 解:(1)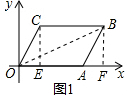 如图1,作CE⊥OA于E,BF⊥OA交x轴于F,
如图1,作CE⊥OA于E,BF⊥OA交x轴于F,
∵∠AOC=60°,OC=4cm,
∴OE=2cm,CE=2$\sqrt{3}$cm,
∴点C的坐标是(2,2$\sqrt{3}$),
∵OC∥AB,
∴∠BAF=∠AOC=60°,AB=OC=4cm,
∴AF=2cm,
∴OF=10cm,又BF=CE=2$\sqrt{3}$cm,
∴OB=$\sqrt{O{F}^{2}+B{F}^{2}}$=4$\sqrt{7}$cm,
故答案为:2;2$\sqrt{3}$;4$\sqrt{7}$;
(2)当0<t≤4时,如图2,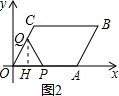 作QH⊥OA于H,
作QH⊥OA于H,
∵∠AOC=60°,OQ=t,
∴QH=$\frac{\sqrt{3}}{2}$t,
S=$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{4}$t2;
当4≤t≤8时,如图2,作QG⊥OA于G,
S=$\frac{1}{2}$×2$\sqrt{3}$×t=$\sqrt{3}$t;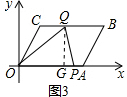 当8≤t<12时,如图4,
当8≤t<12时,如图4,
延长QP交x轴于M,作PN⊥x轴于N,
∵BQ=12-t,BP=12-t,∠B=∠AOC=60°,
∴△BQP是等边三角形,则△PAM为等边三角形,
∵AP=t-8,∠BAM=60°,
∴PN=$\frac{\sqrt{3}}{2}$(t-8),
△OQM的面积=$\frac{1}{2}$×t×2$\sqrt{3}$=$\sqrt{3}$t,
△OPM的面积=$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$(t-8)=$\frac{\sqrt{3}}{4}$t(t-8),
∴S=△OQM的面积-△OPM的面积=-$\frac{\sqrt{3}}{4}$t2+3$\sqrt{3}$t,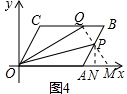
当0<t≤4时,面积最大是4$\sqrt{3}$,
当4≤t≤8时,面积最大是8$\sqrt{3}$,
当8≤t<12时,S=-$\frac{\sqrt{3}}{4}$t2+3$\sqrt{3}$t,面积最大是8$\sqrt{3}$,此时t=8,
∴当t=8时,S的值最大.
点评 本题考查的是平行四边形的性质和函数的知识,掌握平行四边形的对边平行且相等以及等边三角形的性质、锐角三角函数的概念是解题的关键,注意分情况讨论思想的应用.

| A. | 1 | B. | 2 | C. | 1或2 | D. | 0 |
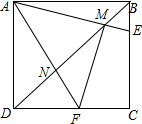 已知正方形ABCD是一个正方形,E是BC上一点,F是CD上一点,∠EAF=45°,AE、AF分别交BD于M、N,连接MF,求证:AM⊥MF,AM=MF.
已知正方形ABCD是一个正方形,E是BC上一点,F是CD上一点,∠EAF=45°,AE、AF分别交BD于M、N,连接MF,求证:AM⊥MF,AM=MF.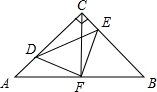 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.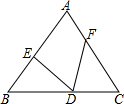 已知,如图,等腰△ABC中,AB=AC,BE=CD,BD=CF.
已知,如图,等腰△ABC中,AB=AC,BE=CD,BD=CF.