题目内容
4.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:| x | … | -1 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 0 | -1 | 0 | 3 | … |
(2)若点(x1,y1)、(x2,y2)都在该函数图象上,当x1<x2<2时,则y1>y2(填“<”“>”或“=”号).
分析 (1)设一般式y=ax2+bx+c,再把表中三组对应值代入得到关于a、b、c的方程组,然后解方程求出a、b、c即可得到解析式,令x=0,求得y=3,得出图象与y轴的交点坐标(0,3),把解析式化成顶点式求得顶点坐标;
(2)根据二次函数的性质求解即可.
解答 解:(1)把(1,0),(3,0),(2,-1)代入y=ax2+bx+c,
得$\left\{\begin{array}{l}{a+b+c=0}\\{9a+3b+c=0}\\{4a+2b+c=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$.
所以抛物线解析式为y=x2-4x+3,
令x=0,y=3,
∵图象与y轴的交点坐标是(0,3),
∵y=x2-4x+3=(x-2)2-1,
∴顶点坐标为(2,-1);
(2)抛物线的对称轴为直线x=2,
因为抛物线开口向上,
所以当x1<x2<2,y1>y2.
故答案为:(0,3),(2,-1),y=x2-4x+3;>.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
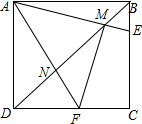 已知正方形ABCD是一个正方形,E是BC上一点,F是CD上一点,∠EAF=45°,AE、AF分别交BD于M、N,连接MF,求证:AM⊥MF,AM=MF.
已知正方形ABCD是一个正方形,E是BC上一点,F是CD上一点,∠EAF=45°,AE、AF分别交BD于M、N,连接MF,求证:AM⊥MF,AM=MF.