题目内容
9．下列式子①7＞4；②3x≥2π+1；③x+y＞1；④x2+3＞2x；⑤$\frac{1}{x}$＞4中，是一元一次不等式的有（ ）| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
分析 根据一元一次不等式的定义求解即可．
解答 解：②3x≥2π+1是一元一次不等式，
故选：D．
点评 本题考查一元一次不等式的定义中的未知数的最高次数为1次，本题还要注意未知数的系数不能是0．
练习册系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
19．若x、y为实数，且$\sqrt{2x-1}$$+\sqrt{1-2x}$+y=4，则xy的值是（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | 2 | D． | 4 |
20．要使$\sqrt{9+2x}$在实数范围内有意义，则（ ）
| A． | x为任何值 | B． | x≤-$\frac{9}{2}$ | C． | x≥$\frac{9}{2}$ | D． | x≥-$\frac{9}{2}$ |
4．201718的个位上的数字是（ ）
| A． | 7 | B． | 3 | C． | 9 | D． | 1 |
14．如果把分式$\frac{xy}{x+y}$（xy≠0）中的x，y都扩大2倍，那么分式的值（ ）
| A． | 变为原来的2倍 | B． | 变为原来的4倍 | C． | 变为原来的8倍 | D． | 不变 |
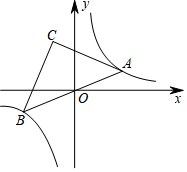如图，点A在双曲线y=$\frac{k}{x}$（k＞0）第一象限分支上，连接AO并延长交另一支于点B，以AB为斜边作等腰直角三角形ABC，已知点C坐标为（-3，7），则k的值为21．
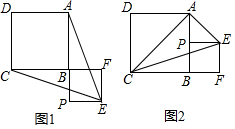已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．