Question

18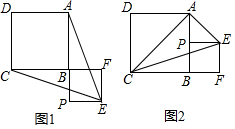．已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA、EC．
（1）如图1，若点P在线段AB的延长线上，求证：EA=EC；
（2）如图2，若点P在线段AB上．连接AC，当P为AB的中点时，判断△ACE的形状，并说明理由．

Answer 1

分析 （1）根据正方形的性质证明△APE≌△CFE，可得结论；
（2）分别证明∠PAE=45°和∠BAC=45°，则∠CAE=90°，即△ACE是直角三角形；

解答 证明：（1）∵四边形ABCD和四边形BPEF是正方形，
∴AB=BC，BP=BF，
∴AP=CF，
在△APE和△CFE中，
∵$\left\{\begin{array}{l}{AP=CF}\\{∠P=∠F}\\{PE=EF}\end{array}\right.$，
∴△APE≌△CFE，
∴EA=EC；

（2）△ACE是直角三角形，
理由是：如图2中，∵P为AB的中点，
∴PA=PB，
∵PB=PE，
∴PA=PE，
∴∠PAE=45°，
又∵∠BAC=45°，
∴∠CAE=90°，即△ACE是直角三角形；

点评 本题是四边形的综合题，考查了正方形的性质、平行线分线段成比例定理、角平分线的逆定理、等腰直角三角形的性质和判定等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．