题目内容
8.我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释a2+2ab+b2=(a+b)2,实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.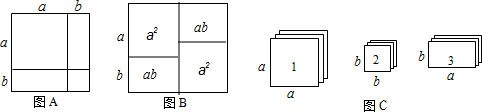
(1)图B可以解释的代数恒等式是2a2+2ab=2a(a+b).
(2)现有足够多的正方形和矩形卡片(如图C),试在下面的虚线方框中画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形(每两张纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使该矩形的面积为a2+ab-2b2,并利用你所画的图形面积对a2+ab-2b2进行因式分解.

分析 (1)看图即可得出所求的式子;
(2)通过画图能更好的理解题意,从而得出结果.由于构成的是正方形,它的面积等于所给图片的面积之和,从而画出图形.
解答 解:(1)2a2+2ab=2a(a+b);
(2)画图如下: ;
;
a2+ab-2b2=(a+2b)(a-b).
点评 本题考查了完全平方公式和几何图形的应用,主要考查学生的画图能力,计算能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.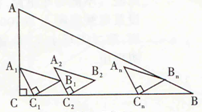 如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
 如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )
如图,在△ABC中,∠C=90°,AC=2,BC=4.△A1B1C1、△A2B2C2、△A3B3C3、…、△AnBnCn是n个相同的等腰直角三角形,其直角顶点C1、C2、C3、…、Cn都在CB边上,点A1在AC上,A2C2经过点B1且平行于A1C1,A3C3经过点B2且平行于A2C2,…,AnCn过点Bn-1且平行于An-1Cn-1,且A1C=2CC1.当n=7时,点B7正好落在AB边,则这个小的等腰直角三角形的直角边长为( )| A. | $\frac{1}{7}$ | B. | $\frac{\sqrt{5}}{7}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{8\sqrt{5}}{5}$ |
17.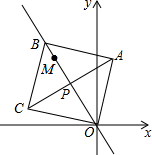 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )| A. | ($\frac{3}{2}$,$\frac{65}{6}$) | B. | ($\sqrt{7}$,11) | C. | (2,2$\sqrt{31}$) | D. | ($\frac{8}{5}$,$\frac{56}{5}$) |
18.已知a为任意整数,且(a+13)2-a2的值总可以被n(n为自然数,且n≠1)整除,则n的值为( )
| A. | 13 | B. | 26 | C. | 13或26 | D. | 13的倍数 |
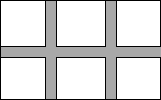 华泰新村开发商为促销商品房,决定在新村所在地的一块60m×100m的长方形空地上种植花草,且铺设三条如图所示的鹅卵石甬道,已知修建甬道后,剩下的草地面积为5568m2,求甬道的宽.
华泰新村开发商为促销商品房,决定在新村所在地的一块60m×100m的长方形空地上种植花草,且铺设三条如图所示的鹅卵石甬道,已知修建甬道后,剩下的草地面积为5568m2,求甬道的宽.
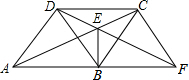 如图,四边形ABCD是菱形,点E为对角线AC上一点,连接DE并延长交AB延长线于点F.连接CF、BD、BE
如图,四边形ABCD是菱形,点E为对角线AC上一点,连接DE并延长交AB延长线于点F.连接CF、BD、BE