题目内容
20.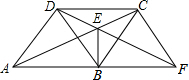 如图,四边形ABCD是菱形,点E为对角线AC上一点,连接DE并延长交AB延长线于点F.连接CF、BD、BE
如图,四边形ABCD是菱形,点E为对角线AC上一点,连接DE并延长交AB延长线于点F.连接CF、BD、BE(1)求证:∠AFD=∠EBC;
(2)若E为△BCD的重心,求∠ACF的度数.
分析 (1)由菱形的性质可证明△CBE≌△CDE,可得∠CDE=∠EBC,再结合平行线的性质可证得∠AFD=∠EBC;
(2)设DF交BC于点P,AC交BD于点O,可证明△DCP≌△FBP,可证明四边形BFCD为平行四边形,结合AC⊥BD,可求得∠ACF=90°.
解答 (1)证明:∵四边形ABCD为菱形,
∴DC=BC,∠DCE=∠BCE,
在△DCE和△BCE中,
$\left\{\begin{array}{l}{DC=BC}\\{∠DCE=∠BCE}\\{CE=CE}\end{array}\right.$,
∴△DCE≌△BCE(SAS),
∴∠EBC=∠EDC,
又∵AB∥CD,
∴∠AFD=∠EDC,
∴∠AFD=∠EBC;
(2)解:如图,设DF交BC于点P,AC交BD于点O,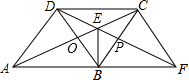
∵E为△BCD的重心,
∴P为BC中点,
∴BP=CP,
在△CPD和△BPF中,
$\left\{\begin{array}{l}{∠CDP=∠PFB}\\{∠CPD=∠BPF}\\{PC=PB}\end{array}\right.$,
∴△CDP≌△BPF(AAS),
∴DP=FP,
∴四边形BFCD是平行四边形,
∴FC∥BD,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOB=90°,
∴∠ACF=∠AOB=90°.
点评 本题主要考查菱形的性质和全等三角形的判定和性质,在(1)中证得三角形全等是解题的关键,在(2)中证明四边形BFCD为平行四边形是解题的关键,注意灵活运用SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
9.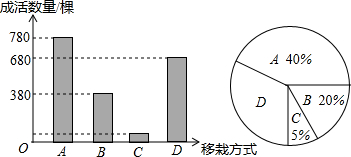 某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
根据以上信息,解答下列问题:
(1)图2中,D种移栽方式所占的圆心角的度数为126°,D种移栽方式的树木有700棵;
(2)请指出图1中存在的错误,并说明理由;
(3)在四种移栽方式中,从所有成活的树木中随机抽取一棵,则这棵树采用B种移栽方式移栽的概率是多少?
 某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确.
某园林部门为扩大绿化面积,进行了大量树木的移栽,他们选择A、B、C、D四种方式对2000棵树进行移栽,并分别统计四种移栽方式的成活情况,旨在提高来年移栽树木的成活率,通过计算制成下表以及两个统计图,经确认图甲有误,其它正确. | 移栽方式 | A | B | C | D |
| 成活率 | 97.5% | 95% | 60% | 90% |
(1)图2中,D种移栽方式所占的圆心角的度数为126°,D种移栽方式的树木有700棵;
(2)请指出图1中存在的错误,并说明理由;
(3)在四种移栽方式中,从所有成活的树木中随机抽取一棵,则这棵树采用B种移栽方式移栽的概率是多少?