题目内容
15．把（x-1）6展开得a6x6+a5x5+…+a2x2+a1x+a0，求a0+a2+a4+a6的值．分析 将x=1代入代数式得a6x6+a5x5+…+a2x2+a1x+a0=a6+a5+…+a2+a1+a0=0，将x=-1代入得：a6x6+a5x5+…+a2x2+a1x+a0=a6-a5+…+a2-a1+a0=64，最后将两式相加，从而可求得a0+a2+a4+a6的值．
解答 解：将x=1代入得：（x-1）6=（1-1）6=0，即a6+a5+…+a2+a1+a0=0①，
将x=-1代入得：：（x-1）6=（-1-1）6=64，即a6-a5+a4-a3+a2-a1+a0=64②，
①+②得：2（a0+a2+a4+a6）=64，
∴a0+a2+a4+a6=32．
点评 本题主要考查得是代数式的求值问题，将x=1，x=-1代入求得a6+a5+…+a2+a1+a0=0和a6-a5+a4-a3+a2-a1+a0=64是解题的关键．
练习册系列答案
相关题目
5．
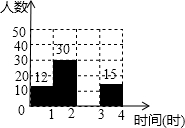阅读对人的影响是巨大的，一本好书往往能改变一个人的一生．某校为了解全校1800名学生双休日的阅读时间，学校随机调查了七、八、九年级部分同学，并用得到的数据绘制成不完整的统计图表如图所示：
（1）x=40，y=0.18；
（2）请将频数分布直方图补充完整；
（3）根据调查数据估计，该校同学双休日阅读时间在2小时以上的学生的人数．
阅读对人的影响是巨大的，一本好书往往能改变一个人的一生．某校为了解全校1800名学生双休日的阅读时间，学校随机调查了七、八、九年级部分同学，并用得到的数据绘制成不完整的统计图表如图所示：| 阅读时间 | 频数（人数） | 频率 |
| 0～1 | 12 | 0.12 |
| 1～2 | 30 | 0.3 |
| 2～3 | x | 0.4 |
| 3～4 | 18 | y |
| 合计 | m | 1 |
（2）请将频数分布直方图补充完整；
（3）根据调查数据估计，该校同学双休日阅读时间在2小时以上的学生的人数．
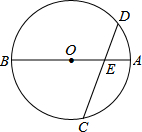如图，AB为⊙O的直径，弦CD与AB相交于点E，且OE=DE，试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系．
3．在（-2），（-2）3，|-2|，（-2）2，-22中，负数有（ ）个．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
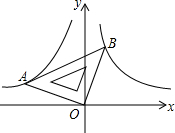如图，一块等腰直角三角板AOB的直角顶点O与坐标原点生命，点B、A分别在第一、二象限，反比例函数y=$\frac{{k}_{1}}{x}$、y=$\frac{{k}_{2}}{x}$的图象分别经过点A、B，若点A的坐标是（-3，1），分别求出k1，k2的值．