��Ŀ����
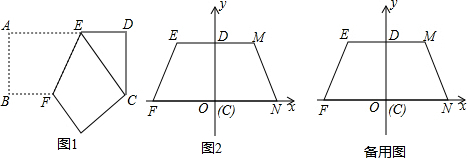
��ͼ1���ھ���ABCD�У���֪AB=4��BC=8���ֽ��˾����۵���ʹ��A��C�غϣ�Ȼ�����ۺ�EF�ÿ����õ�����ֱ�����Σ�������ƴ��һ�𣬷�����ƽ��ֱ������ϵ�ڣ���ͼ2��ʾ��
��1����ͼ2������EFNM����������꣮
��2������P�ӵ�M��������ÿ��1����λ���ٶȣ����E�˶�������Q�ӵ�F��������ÿ��a����λ���ٶȣ����N����������P��Qͬʱ��������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��s����
����a=2���ʣ��Ƿ����������t��ʹ��ֱ��PQ������EFNM������ֳ�1��2�����֣������ڣ���������п��ܵ�t��ֵ���������ڣ���˵�����ɣ�
���Ƿ����������a��ʹ���˶������У�����������t��ʹ����P��E��Q��OΪ������ı���Ϊ���Σ������ڣ���������з���������a��ֵ���������ڣ���˵�����ɣ�
��1����ͼ2������EFNM����������꣮
��2������P�ӵ�M��������ÿ��1����λ���ٶȣ����E�˶�������Q�ӵ�F��������ÿ��a����λ���ٶȣ����N����������P��Qͬʱ��������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt��s����
����a=2���ʣ��Ƿ����������t��ʹ��ֱ��PQ������EFNM������ֳ�1��2�����֣������ڣ���������п��ܵ�t��ֵ���������ڣ���˵�����ɣ�
���Ƿ����������a��ʹ���˶������У�����������t��ʹ����P��E��Q��OΪ������ı���Ϊ���Σ������ڣ���������з���������a��ֵ���������ڣ���˵�����ɣ�

���㣺�ı����ۺ���
ר�⣺
��������1����DE=x����Rt��CDE�����ù��ɶ��������x���ٵ�AE��CF�ij������ɵ�����EFNM����������ꣻ
��2���������S����EFNM=S����ABCD=32��ֱ��PQ������EFNM������ֳ�1��2�����֣���S�ı���EFQP��S�ı���PQNM=1��2��S�ı���EFQP��S�ı���PQNM=2��1������������ۣ�
�ڵ�һ�����Σ���EPQOΪ���Σ���EO=5������ON=5����Q�˶���N����OQ=5��ֻҪ����EP=5�����֤�ı���EPQOΪ���Σ��ڶ������Σ���EQOPΪ���Σ���Rt��OPD�У��ɹ��ɶ�����t=
�������a��ֵ��
��2���������S����EFNM=S����ABCD=32��ֱ��PQ������EFNM������ֳ�1��2�����֣���S�ı���EFQP��S�ı���PQNM=1��2��S�ı���EFQP��S�ı���PQNM=2��1������������ۣ�
�ڵ�һ�����Σ���EPQOΪ���Σ���EO=5������ON=5����Q�˶���N����OQ=5��ֻҪ����EP=5�����֤�ı���EPQOΪ���Σ��ڶ������Σ���EQOPΪ���Σ���Rt��OPD�У��ɹ��ɶ�����t=
| 11 |
| 6 |
����⣺��1����DE=x����CE=AE=8-x��
����Rt��CDE�����ù��ɶ�������ã�42+x2=��8-x��2��
x=3��8-3=5��
��E��-3��4����M��3��4����F��-5��0����N��5��0����
��2���١ߵ�a=2ʱ��MP=t��QN=10-2t��S����EFNM=S����ABCD=32��
��S�ı���EFQP��S�ı���PQNM=1��2��
��
=1��2
�ɵ�t=-
����ȥ��
��S�ı���EFQP��S�ı���PQNM=2��1��
��
=2��1
�ɵ�t=
��
����a=2����t=
ʱ��ֱ��PQ������EFNM������ֳ�1��2�����֣�
�ڵ�һ�����Σ���EPQOΪ���Σ��������EO=5������ON=5��
��Q�˶���N����OQ=5��
�֡�EP��OQ��ֻҪ����EP=5�����֤�ı���EPQOΪ���Σ�
��EP=6-t=5���ɵ�t=1����ʱ�������a=10��
�ڶ������Σ���EQOPΪ���Σ���DP=3-t��OP=EP=6-t��
��Rt��OPD�У��ɹ��ɶ�����t=
��
��QO=EP=6-
=
���ɵ�FQ=5-QO=
��
�����������£�a=
��
=
��
����ڷ���������a=10��a=
��ʹ����P��E��Q��OΪ������ı���Ϊ���Σ�
����Rt��CDE�����ù��ɶ�������ã�42+x2=��8-x��2��
x=3��8-3=5��
��E��-3��4����M��3��4����F��-5��0����N��5��0����
��2���١ߵ�a=2ʱ��MP=t��QN=10-2t��S����EFNM=S����ABCD=32��
��S�ı���EFQP��S�ı���PQNM=1��2��
| (6-t+2t)��4 |
| 2 |
| (t+10-2t)��4 |
| 2 |
�ɵ�t=-
| 2 |
| 3 |
��S�ı���EFQP��S�ı���PQNM=2��1��
| (6-t+2t)��4 |
| 2 |
| (t+10-2t) |
| 2 |
�ɵ�t=
| 14 |
| 3 |
����a=2����t=
| 14 |
| 3 |
�ڵ�һ�����Σ���EPQOΪ���Σ��������EO=5������ON=5��
��Q�˶���N����OQ=5��
�֡�EP��OQ��ֻҪ����EP=5�����֤�ı���EPQOΪ���Σ�
��EP=6-t=5���ɵ�t=1����ʱ�������a=10��
�ڶ������Σ���EQOPΪ���Σ���DP=3-t��OP=EP=6-t��
��Rt��OPD�У��ɹ��ɶ�����t=
| 11 |
| 6 |
��QO=EP=6-
| 11 |
| 6 |
| 25 |
| 6 |
| 5 |
| 6 |
�����������£�a=
| 5 |
| 6 |
| 11 |
| 6 |
| 5 |
| 11 |
����ڷ���������a=10��a=
| 5 |
| 11 |
������������Ҫ�������ı��ε��ۺ��⣬�õ��۵������ʣ����ɶ������Լ����ε��ж����ѶȽϴ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
�������Ρ����Ρ����Ρ�ƽ���ı����У���Գ�ͼ�ε��У�����������
| A��1 | B��2 | C��3 | D��4 |
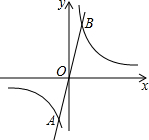 ��ͼ����֪����������y=
��ͼ����֪����������y= ��ͼ����֪������ABCD�е�A��1��2����B��3��5����C��4��3����С��ͬѧ�ڻ���ͼ��С�İ�������������ˣ������������x�ᣬy�ἰԭ�㣬������������ABC�������
��ͼ����֪������ABCD�е�A��1��2����B��3��5����C��4��3����С��ͬѧ�ڻ���ͼ��С�İ�������������ˣ������������x�ᣬy�ἰԭ�㣬������������ABC������� ��ͼ����?ABCD�У�F��AD���е㣬�ӳ�BC����E��ʹCE=
��ͼ����?ABCD�У�F��AD���е㣬�ӳ�BC����E��ʹCE=