题目内容
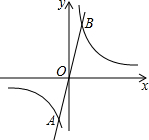 如图,已知反比例函数y=
如图,已知反比例函数y=| 2 |
| x |
(1)求正比例函数的解析式及两函数图象另一个交点B的坐标;
(2)试根据图象写出不等式
| 2 |
| x |
(3)在反比例函数图象上是否存在点C,使△OAC为等边三角形?若存在,求出点C的坐标;若不存在,请说明理由.
考点:反比例函数与一次函数的交点问题
专题:代数综合题,数形结合
分析:(1)把点A的坐标代入y=
求出m的值,再运用A的坐标求出k,两函数解析式联立得出B点的坐标.
(2)把k的值代入不等式,讨论当a>0和当a<0时分别求出不等式的解.
(3)讨论当C在第一象限时,△OAC不可能为等边三角形,当C在第三象限时,根据OA=OC,求出点C的坐标,再看AC的值看是否构成等边三角形.
| 2 |
| x |
(2)把k的值代入不等式,讨论当a>0和当a<0时分别求出不等式的解.
(3)讨论当C在第一象限时,△OAC不可能为等边三角形,当C在第三象限时,根据OA=OC,求出点C的坐标,再看AC的值看是否构成等边三角形.
解答:解:(1)把A(m,-2)代入y=
,得-2=
,
解得m=-1,
∴A(-1,-2)代入y=kx,
∴-2=k×(-1),解得,k=2,
∴y=2x,
又由2x=
,得x=1或x=-1(舍去),
∴B(1,2),
(2)∵k=2,
∴
≥kx为
≥2x,
根据图象可得:当x≤-1和0<x≤1时,反比例函数y=
的图象恒在正比例函数y=2x图象的上方,即
≥2x.
(3)①当点C在第一象限时,△OAC不可能为等边三角形,
②如图,当C在第三象限时,要使△OAC为等边三角形,则OA=OC,设C(t,
)(t<0),
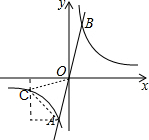
∵A(-1,-2)
∴OA=
∴t2+
=5,则t4-5t2+4=0,
∴t2=1,t=-1,此时C与A重合,舍去,
t2=4,t=-2,∴C(-2,-1),而此时AC=
,AC≠AO,
∴不存在符合条件的点C.
| 2 |
| x |
| 2 |
| m |
解得m=-1,
∴A(-1,-2)代入y=kx,
∴-2=k×(-1),解得,k=2,
∴y=2x,
又由2x=
| 2 |
| x |
∴B(1,2),
(2)∵k=2,
∴
| 2 |
| x |
| 2 |
| x |
根据图象可得:当x≤-1和0<x≤1时,反比例函数y=
| 2 |
| x |
| 2 |
| x |
(3)①当点C在第一象限时,△OAC不可能为等边三角形,
②如图,当C在第三象限时,要使△OAC为等边三角形,则OA=OC,设C(t,
| 2 |
| t |

∵A(-1,-2)
∴OA=
| 5 |
∴t2+
| 4 |
| t2 |
∴t2=1,t=-1,此时C与A重合,舍去,
t2=4,t=-2,∴C(-2,-1),而此时AC=
| 2 |
∴不存在符合条件的点C.
点评:本题主要考查了反比例函数与一次函数的交点问题,解题的关键是求出点C的坐标,看是否构成等边三角形.

练习册系列答案
相关题目
一辆汽车在笔直的公路上行驶,在两次转弯后,前进的方向仍与原来相同,那么这两次转弯的角度可以是( )
| A、先右转60°,再左转120° |
| B、先左转120°,再右转120° |
| C、先左转60°,再左转120° |
| D、先右转60°,再右转60° |
已知28a2bm÷4anb2=7b2,那么m、n的值为( )
| A、m=4,n=2 |
| B、m=4,n=1 |
| C、m=1,n=2 |
| D、m=2,n=2 |
(
)2004×(-1.6)2005÷(-1)2003=( )
| 5 |
| 8 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC上运动(点E不与A、C重合),且保持AE=CF,连接DE、DF、EF,在运动变化过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC上运动(点E不与A、C重合),且保持AE=CF,连接DE、DF、EF,在运动变化过程中,有下列结论: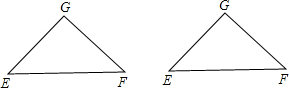
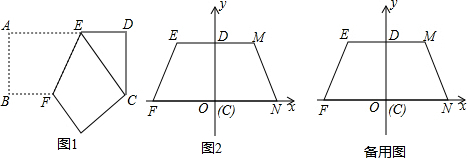
 小明想把一长为60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.
小明想把一长为60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个相同的小正方形.