题目内容
15.在学校乒乓球比赛中,从陈亮、李明、刘松、周杰、王刚这五人中,随机抽签一组对手,正好抽到王刚与刘松的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与正好抽到王刚与刘松的情况,再利用概率公式即可求得答案.
解答 解:画树状图得: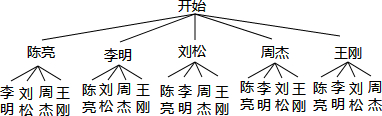
∵共有20种等可能的结果,正好抽到王刚与刘松的有2种情况,
∴正好抽到王刚与刘松的概率是:$\frac{2}{20}$=$\frac{1}{10}$.
故选C.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
20.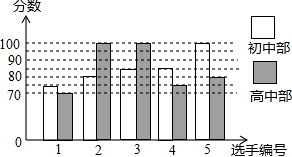 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
求得初中代表队选手决赛成绩的平均数和方差:
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85,
${{S}_{1}}^{2}$=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70;
(1)根据图示填写表格:
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.求得初中代表队选手决赛成绩的平均数和方差:
$\overline{{x}_{1}}$=$\frac{75+80+85+85+100}{5}$=85,
${{S}_{1}}^{2}$=$\frac{1}{5}$[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70;
(1)根据图示填写表格:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
(3)计算高中代表队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
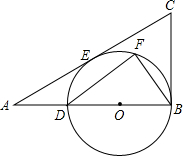 如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.
如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E. 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).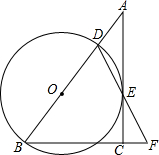 在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.
在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O.与AC相切于点E,连结DE并延长与BC的延长线交于点F.