题目内容
5. 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
分析 连接OB,如图,利用切线的性质得到∠OAP=∠OBP=90°,再利用四边形内角和计算出∠AOB的度数,然后根据等腰三角形的性质和三角形外角性质求∠ACB的度数.
解答 解:连接OB,如图,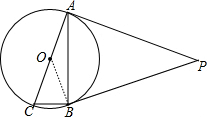 ∵PA、PB是⊙O的切线,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-50°=130°,
∵OB=OC,
∴∠OCB=∠OBC,
而∠AOB=∠OCB+∠OBC,
∴∠OCB=$\frac{1}{2}$×130°=65°,
即∠ACB=65°.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.解决本题的关键是求出∠AOB的度数.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
16.若一个多边形的每个内角都是120°,这个多边形是( )
| A. | 八角形 | B. | 七边形 | C. | 五边形 | D. | 六边形 |
13.下面计算中,正确的是( )
| A. | (-2mn)3=8m3n3 | B. | (m+n)3(m+n)2=m5+n5 | C. | -(a3b2)3=-a9b6 | D. | (-$\frac{1}{3}$a4b)2=$\frac{1}{6}$a6b2 |
15.在学校乒乓球比赛中,从陈亮、李明、刘松、周杰、王刚这五人中,随机抽签一组对手,正好抽到王刚与刘松的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
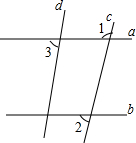 如图,已知∠1=98°,∠2=∠3=82°,试说明:a∥b,c∥d.
如图,已知∠1=98°,∠2=∠3=82°,试说明:a∥b,c∥d.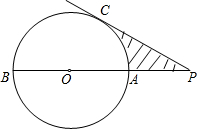 如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).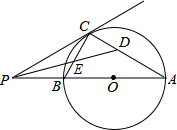 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.
如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连结AC,BC.作∠APC的平分线交AC于点D,交BC于点E.