题目内容
3. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有①③⑤(填序号).
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有①③⑤(填序号).
分析 通过条件可以得出△ABE≌△ADF,从而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC,就可以得出AC垂直平分EF,设EC=x,BE=y,由勾股定理就可以得出x与y的关系,表示出BE与EF,于是得到结论.
解答 解:∵四边形ABCD是正方形,△AEF是等边三角形,
∴AB=AD,AE=AF,∠B=∠D,=90°,
在Rt△ABE和Rt△ADF中,$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF,
∴BE=DF,故①正确,
∵BC=DC,
∴CE=CF,
∴⑤△CEF为等腰直角三角形,
由于AE=AF,CW=CF,
∴AC垂直平分EF,故③⑤正确,
∵△AEF是等边三角形,∴∠AEF=60°,故②错误,
设EC=x,由勾股定理,得
EF=$\sqrt{2}$x,CG=$\frac{\sqrt{2}}{2}$x,
AG=AEsin60°=EFsin60°=2×CGsin60°=$\frac{\sqrt{6}}{2}$x,
∴AC=$\frac{\sqrt{6}x+\sqrt{2}x}{2}$,
∴AB=$\frac{\sqrt{3}x+x}{2}$,
∴BE=$\frac{\sqrt{3}x+x}{2}$-x=$\frac{\sqrt{3}x-x}{2}$,
∴BE+DF=$\sqrt{3}$x-x≠$\sqrt{2}$x,故④错误,
故答案为:①③⑤.
点评 本题主要考查了全等三角形的判断和性质,等边三角形和正方形的性质,线段垂直平分线的性质和判定,证得Rt△ABE≌Rt△ADF是解题的关键.

练习册系列答案
相关题目
13.在平面直角坐标系中,点A,B的坐标分别为(2m-2,3),(m,3),且点A在点B的左侧,若线段AB与直线y=-2x+1相交,则m的取值范围是( )
| A. | -1≤m≤$\frac{1}{2}$ | B. | -1≤m≤1 | C. | -$\frac{1}{2}$≤m≤1 | D. | 0≤m≤1 |
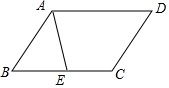 如图,平行四边形ABCD中,AD=5,AB=3,若AE平分∠BAD交边BC于点E,则线段EC的长度为2.
如图,平行四边形ABCD中,AD=5,AB=3,若AE平分∠BAD交边BC于点E,则线段EC的长度为2.