��Ŀ����
13����1�����Ķ�������գ���x+5����x+6��=x2+11x+30��
��x-5����x-6��=x2-11x+30��
��x-5����x+6��=x2+x-30��
��x+5����x-6��=x2-x-30��
�۲��������ʽ�����ݹ��ɣ�ֱ��д�����и�ʽ�Ľ����
��a+90����a-100��=a2-10a-9000�� ��y-80����y-90��=y2-170y+7200��
��2�����Ķ�������գ���x-1����x+1��=x2-1����x-1����x2+x+1��=x3-1����x-1����x3+x2+x+1��=x4-1����x-1����x4+x3+x2+x+1��=x5-1��
�۲������ʽ�����ɴ˹��ɳ�һ���Թ��ɣ���x-1����xn-1+xn-2+xn-3+��+x2+x+1��=xn-1��
�ڸ��ݢ�ֱ��д��1+3+32+��+367+368�Ľ��$\frac{{3}^{69}-1}{2}$��
���� ��1�����ݣ�x+p����x+q��=x2+��p+q��x+pq�ɵã�
��2��������֪��ʽ�ɵã�x-1����xn-1+xn-2+xn-3+��+x2+x+1��=xn-1���ڽ�ԭʽ����Ϊ$\frac{1}{2}$����3-1������1+3+32+��+367+368���������â������ù������ɵã�
��� �⣺��1���ߣ�x+5����x+6��=x2+��5+6��x+5��6=x2+11x+30��
��x-5����x-6��=x2+��-5-6��x+��-5������-6��=x2-11x+30��
��x-5����x+6��=x2+��-5+6��x+��-5����6=x2+x-30��
��x+5����x-6��=x2+��5-6��x+5����-6��=x2-x-30��
�ࣨa+90����a-100��=a2+��90-100��a+90����-100��=a2-10a-9000��
��y-80����y-90��=y2+��-80-90��y+��-80������-90��=y2-170y+7200��
�ʴ�Ϊ��a2-10a-9000��y2-170y+7200��
��2����������֪����x-1����xn-1+xn-2+xn-3+��+x2+x+1��=xn-1��
�ʴ�Ϊ��xn-1��
��ԭʽ=$\frac{1}{2}$����3-1������1+3+32+��+367+368��=$\frac{1}{2}$����369-1����
�ʴ�Ϊ��$\frac{{3}^{69}-1}{2}$��
���� ������Ҫ�������ֵı仯���ɣ�������֪��ʽ�ó�һ������ǽ���Ĺؼ���

 ��ͼ��ͼ1����5����ȫ��ͬ���������ɵļ����壬�ֽ�����E��������ƽ����ͼ2��ʾ��λ�ã�����˵������ȷ���ǣ�������
��ͼ��ͼ1����5����ȫ��ͬ���������ɵļ����壬�ֽ�����E��������ƽ����ͼ2��ʾ��λ�ã�����˵������ȷ���ǣ����������������������������ͼ��ͬ
����������������ĸ���ͼ��ͬ
���������������������ͼ��ͬ��
| A�� | �٢ڢ� | B�� | �ڢ� | C�� | �٢� | D�� | �٢� |
 ��ͼ���ڡ�ABC�У�BD��CE�ǡ�ABC�����ߣ�BD��CE�ཻ�ڵ�0����F��G�ֱ���BO��CO���е㣬����AO����AO=6cm��BC=8cm�����ı���DEFG���ܳ��ǣ�������
��ͼ���ڡ�ABC�У�BD��CE�ǡ�ABC�����ߣ�BD��CE�ཻ�ڵ�0����F��G�ֱ���BO��CO���е㣬����AO����AO=6cm��BC=8cm�����ı���DEFG���ܳ��ǣ�������| A�� | 14 cm | B�� | 18 cm | C�� | 24 cm | D�� | 28 cm |
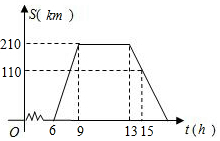 ij����������6ʱ���ùݳ�����������������210km��ij�������ξ������棬���������ùݵľ���S��km����ʱ��t��h���Ĺ�ϵ��������ͼ�����߱�ʾ������ͼ���ṩ���й���Ϣ������������⣺
ij����������6ʱ���ùݳ�����������������210km��ij�������ξ������棬���������ùݵľ���S��km����ʱ��t��h���Ĺ�ϵ��������ͼ�����߱�ʾ������ͼ���ṩ���й���Ϣ������������⣺
 ��ͼ����O��ֱ��AB=5����AC=3����PEF�Ķ����ڡ�ABC�ı��ϣ�EF��CB��PB=2EC����EC=t����PEF�����ΪS��
��ͼ����O��ֱ��AB=5����AC=3����PEF�Ķ����ڡ�ABC�ı��ϣ�EF��CB��PB=2EC����EC=t����PEF�����ΪS�� ��ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G�����н��ۣ���BE=DF���ڡ�AEF=15�㣻��AC��ֱƽ��EF����BE+DF=EF���ݡ�CEFΪ����ֱ�������Σ�������ȷ���Т٢ۢݣ�����ţ���
��ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G�����н��ۣ���BE=DF���ڡ�AEF=15�㣻��AC��ֱƽ��EF����BE+DF=EF���ݡ�CEFΪ����ֱ�������Σ�������ȷ���Т٢ۢݣ�����ţ���