题目内容
18.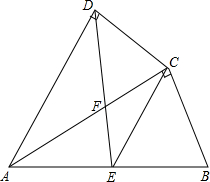 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点连接CE,连接DE交AC于F.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点连接CE,连接DE交AC于F.(1)求证:△ADC∽△ACB;
(2)若AD=6,AB=8,求$\frac{AF}{CF}$的值.
分析 (1)由AC平分∠DAB得∠DAC=∠CAB,加上∠ADC=∠ACB=90°可迅速得出结论;
(2)由于E为AB中点,从而CE=AE,∠EAC=∠ECA,由(1)知∠DAC=∠CAB,得∠DAC=∠ECA,CE∥AD,△AFD∽△CFE,从而$\frac{AD}{CE}=\frac{AF}{CF}$,而AD已知,CE为AB的一半,答案显然.
解答 解:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB;
(2)∵E为AB中点,
∴CE=$\frac{1}{2}$AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE,
∴$\frac{AD}{CE}=\frac{AF}{CF}$,
∵CE=$\frac{1}{2}$AB,
∴CE=$\frac{1}{2}×8=4$,
∵AD=6,
∴$\frac{AF}{CF}=\frac{6}{4}=\frac{3}{2}$.
点评 本题主要考查了相似三角形的判定与性质、直角三角形斜边中线定理,属于基础题.熟练掌握中位线定理与相似三角形的判定与性质是解答的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.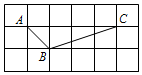 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
 (1)如图,点C是线段AB上一点,D、E分别是AC、BC的中点,已知DE=6,求AB的长;
(1)如图,点C是线段AB上一点,D、E分别是AC、BC的中点,已知DE=6,求AB的长; 如图,在△ABC中,BD为△ABC的角平分线,如果∠A=47°,∠ADB=116°,求∠ABC和∠C的度数.
如图,在△ABC中,BD为△ABC的角平分线,如果∠A=47°,∠ADB=116°,求∠ABC和∠C的度数.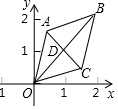 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第50秒时,菱形的对角线交点D的坐标为(-1,1).
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第50秒时,菱形的对角线交点D的坐标为(-1,1).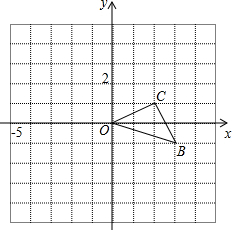 如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,-1)的对称点的坐标为(-6,2).
如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,-1)的对称点的坐标为(-6,2).