题目内容
8.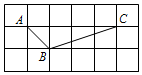 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
分析 构造直角三角形利用正弦函数的定义直接求解即可.
解答  解:如图:BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
解:如图:BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
所以sin∠ACB=$\frac{BD}{BC}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$,
故选C.
点评 本题考查了解直角三角形及勾股定理的知识,解题的关键是根据图形构造直角三角形并利用勾股定理求得BC边的长,难度不大.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.2016年11月27日,“逸仙杯”中山国际马拉松赛在中山市举行,来自18个国家和地区的15 000名参赛者从孙文纪念公园开跑,数量15 000用科学记数法表示为( )
| A. | 15×103 | B. | 1.5×104 | C. | 1.5×103 | D. | 0.15×105 |
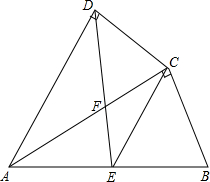 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点连接CE,连接DE交AC于F.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点连接CE,连接DE交AC于F. 如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC=12.
如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC=12.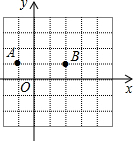 如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有5个.
如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有5个.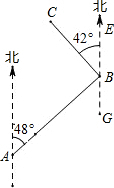 如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长12千米,另一条公路BC长是5千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( )
如图,在A、B 两地之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A,B两地同时开工,若干天后公路准确接通,若公路AB长12千米,另一条公路BC长是5千米,且BC的走向是北偏西42°,则A地到公路BC的距离是( ) 如图,四边形ABCO方形,△BEF是等腰直角三角形,∠EBF=90°,点C,E在x轴上,点A在y轴上,点F在双曲线y=$\frac{k}{x}$(k≠0)第一象限内的图象上,S△BEF=5,OC=1,则k=8.
如图,四边形ABCO方形,△BEF是等腰直角三角形,∠EBF=90°,点C,E在x轴上,点A在y轴上,点F在双曲线y=$\frac{k}{x}$(k≠0)第一象限内的图象上,S△BEF=5,OC=1,则k=8.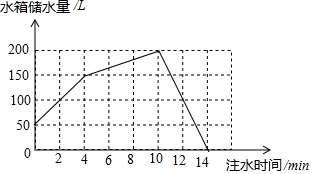 容积为200L的水箱上装有两根进水管A,B和一根排水管C.如图,先由A,B两根进水管同时向水箱内注水,再由B管单独向水箱内注水,最后由C管将水箱内的水排完.
容积为200L的水箱上装有两根进水管A,B和一根排水管C.如图,先由A,B两根进水管同时向水箱内注水,再由B管单独向水箱内注水,最后由C管将水箱内的水排完.