题目内容
20.计算:(1)(-3x+2)(-3x-2)-5x(1-x)+(2x+1)(x-5)
(2)$\frac{{{x^2}-8x+16}}{{{x^2}+2x}}÷(\frac{12}{x+2}-x+2)-\frac{1}{x+4}$.
分析 (1)原式利用平方差公式,单项式乘以多项式,以及多项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式第一项括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后计算即可得到结果.
解答 解:(1)原式=9x2-4-5x+5x2+2x2-9x-5=16x2-14x-9;
(2)原式=$\frac{(x-4)^{2}}{x(x+2)}$÷$\frac{12-(x+2)(x-2)}{x+2}$-$\frac{1}{x+4}$=$\frac{(x-4)^{2}}{x(x+2)}$•$\frac{x+2}{-(x+4)(x-4)}$-$\frac{1}{x+4}$=-$\frac{x-4}{x(x+4)}$-$\frac{x}{x(x+4)}$=-$\frac{-2x+4}{x(x+4)}$.
点评 此题考查了分式的混合运算,以及整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
8.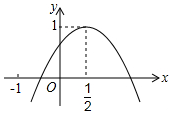 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.在因此女子体操比赛中,8名运动员的年龄(单位:岁)分别为:14,12,12,15,14,15,14,16.这组数据的中位数和方差分别为( )
| A. | 14和2 | B. | 14.5和1.75 | C. | 14和1.75 | D. | 15和2 |
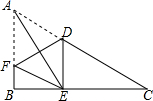 如图,在△ABC中,∠B=90°,点D在AC边上,DE⊥BC于E,将△ABC沿过点D的直线对折,使点A落在BC边上的点E处,折痕交AB于点F.
如图,在△ABC中,∠B=90°,点D在AC边上,DE⊥BC于E,将△ABC沿过点D的直线对折,使点A落在BC边上的点E处,折痕交AB于点F.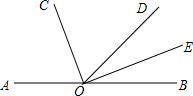 如图,∠AOD与∠BOD互为补角,射线OC、OE分别平分∠AOD和∠BOD.
如图,∠AOD与∠BOD互为补角,射线OC、OE分别平分∠AOD和∠BOD.