题目内容
8.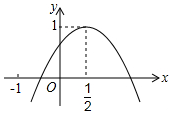 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(0.5,1),下列结论:①ac<0;②a+b=0;③4ac-b2=4a;④(a+c)2-b2<0.其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线开口方向得到a<0,由抛物线与y轴的交点在x轴上方得到c>0,可对①进行判断;由抛物线的对称轴为直线x=-$\frac{b}{2a}$=$\frac{1}{2}$,得到a+b=0,可对②进行判断;根据抛物线的顶点坐标公式可对③进行判断;根据抛物线与x轴交点的各数对②进行判断;根据x=1和x=-1时的函数值的符号,可对④进行判断.
解答 解:①∵抛物线图象开口向下,且与y轴交点在y轴正半轴,
∴a<0,c>0.
∴ac<0,正确;
②∵抛物线顶点坐标为(0.5,1),
∴抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{1}{2}$,
∴a=-b,即a+b=0,正确;
③∵二次函数y=ax2+bx+c的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
∴有$\frac{4ac-{b}^{2}}{4a}$=1,即4ac-b2=4a,正确;
④当x=1时,y=a+b+c>0,
当x=-1时,y=a-b+c<0,
则(a-b+c)(a+b+c)<0,即(a+c)2-b2<0,正确.
正确的有4个.
故选D.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
3.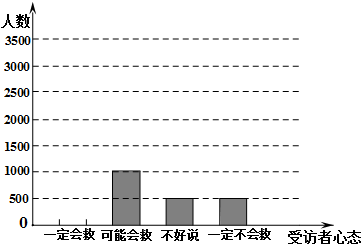 2011年10月13日下午5时30分,在广东佛山南海黄岐镇广佛五金城,两岁的“悦悦”被迎面驶来的面包车撞倒卷到车底.因无人施救,“悦悦”被小型货柜车再次碾压.之后往来的十余个路人均见死不救,直到一位拾荒阿姨看到并救起“悦悦”.“小悦悦事件”发生后,立刻引起全社会的关注与反思.某社会调查中心通过网络,发起“拒绝冷漠,关爱他人”的调查活动,对部分网民进行在线调查.下面是根据调查结果绘制的受访者年龄频数分布表和受访者心态分布直方图(单位:人).读图、表,回答下列问题:(“60后”是指出生在上世纪60年代的人,以下类推)
2011年10月13日下午5时30分,在广东佛山南海黄岐镇广佛五金城,两岁的“悦悦”被迎面驶来的面包车撞倒卷到车底.因无人施救,“悦悦”被小型货柜车再次碾压.之后往来的十余个路人均见死不救,直到一位拾荒阿姨看到并救起“悦悦”.“小悦悦事件”发生后,立刻引起全社会的关注与反思.某社会调查中心通过网络,发起“拒绝冷漠,关爱他人”的调查活动,对部分网民进行在线调查.下面是根据调查结果绘制的受访者年龄频数分布表和受访者心态分布直方图(单位:人).读图、表,回答下列问题:(“60后”是指出生在上世纪60年代的人,以下类推)
(1)频数分布表中,a=0.1,b=1500,c=0.52;不好说可能会救一定会救一定不会救受访者心态人数;
(2)补全受访者心态分布直方图;
(3)如果受访者有10万人,请你估计选择“一定会救”的人数约有多少人?
 2011年10月13日下午5时30分,在广东佛山南海黄岐镇广佛五金城,两岁的“悦悦”被迎面驶来的面包车撞倒卷到车底.因无人施救,“悦悦”被小型货柜车再次碾压.之后往来的十余个路人均见死不救,直到一位拾荒阿姨看到并救起“悦悦”.“小悦悦事件”发生后,立刻引起全社会的关注与反思.某社会调查中心通过网络,发起“拒绝冷漠,关爱他人”的调查活动,对部分网民进行在线调查.下面是根据调查结果绘制的受访者年龄频数分布表和受访者心态分布直方图(单位:人).读图、表,回答下列问题:(“60后”是指出生在上世纪60年代的人,以下类推)
2011年10月13日下午5时30分,在广东佛山南海黄岐镇广佛五金城,两岁的“悦悦”被迎面驶来的面包车撞倒卷到车底.因无人施救,“悦悦”被小型货柜车再次碾压.之后往来的十余个路人均见死不救,直到一位拾荒阿姨看到并救起“悦悦”.“小悦悦事件”发生后,立刻引起全社会的关注与反思.某社会调查中心通过网络,发起“拒绝冷漠,关爱他人”的调查活动,对部分网民进行在线调查.下面是根据调查结果绘制的受访者年龄频数分布表和受访者心态分布直方图(单位:人).读图、表,回答下列问题:(“60后”是指出生在上世纪60年代的人,以下类推) | 分 组 | 频 数 | 频 率 |
| “60后”网民 | 300 | 0.06 |
| “70后”网民 | 500 | a |
| “80后”网民 | b | 0.30 |
| “90后”网民 | 2600 | c |
| 其 它 | 100 | 0.02 |
(2)补全受访者心态分布直方图;
(3)如果受访者有10万人,请你估计选择“一定会救”的人数约有多少人?
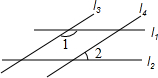 如图:直线l1∥l2,l3∥l4,∠1比∠2的3倍少20°,则∠1=130°,∠2=50°.
如图:直线l1∥l2,l3∥l4,∠1比∠2的3倍少20°,则∠1=130°,∠2=50°.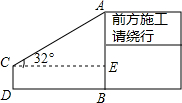 如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)