题目内容
10.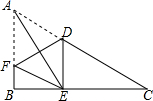 如图,在△ABC中,∠B=90°,点D在AC边上,DE⊥BC于E,将△ABC沿过点D的直线对折,使点A落在BC边上的点E处,折痕交AB于点F.
如图,在△ABC中,∠B=90°,点D在AC边上,DE⊥BC于E,将△ABC沿过点D的直线对折,使点A落在BC边上的点E处,折痕交AB于点F.求证:四边形ADEF是菱形.
分析 设AE与DF的交点为O,如图所示,由折叠可得AE⊥DF,OF=OD,要证四边形ADEF是菱形,只需证OA=OE,只需证△AFO≌△EDO即可.
解答 证明:设AE与DF的交点为O,如图所示,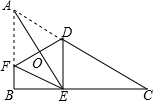
∵∠B=90°,DE⊥BC,
∴∠B=∠DEC=90°,
∴AB∥DE,
∴∠FAO=∠DEO.
由折叠可得:
AE⊥DF,OF=OD.
在△AFO和△EDO中,
$\left\{\begin{array}{l}{∠FAO=∠DEO}\\{∠AOF=∠EOD}\\{OF=OD}\end{array}\right.$,
∴△AFO≌△EDO,
∴OA=OE.
∵OF=OD,OA=OE,AE⊥DF,
∴四边形ADEF是菱形.
点评 本题主要考查了平行线的判定与性质、全等三角形的判定与性质、折叠的性质、菱形的判定等知识,由平行和中点推出三角形全等是解决本题的关键.

练习册系列答案
相关题目
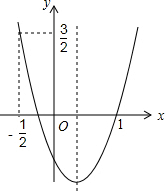 如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④.
如图,二次函数的图象开口向上.图象经过点(-$\frac{1}{2}$,$\frac{3}{2}$)和(1,0)且与y轴交于负半轴.给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是②④. 小明动手操作如下,先剪一个等腰三角形纸片ABC,使AB=AC,再把∠B沿EM折叠,使点B落在点D上;把∠C沿FN折叠,使点C落在点D上,则四边形AEDF是平行四边形,你认为正确吗?请说明理由.
小明动手操作如下,先剪一个等腰三角形纸片ABC,使AB=AC,再把∠B沿EM折叠,使点B落在点D上;把∠C沿FN折叠,使点C落在点D上,则四边形AEDF是平行四边形,你认为正确吗?请说明理由.