题目内容
1.直线y=$\frac{\sqrt{3}}{3}$x+4与x轴交于点A,与y轴交于点B,以AB为边在第二象限内作等边△ABC(1)求点C的坐标;
(2)是否存在点M(m,2)使得△ABM的面积等于△ABC的面积,如存在,求出点M的坐标;不存在,说明理由
(3)若点D(4,0)在直线AB上,是否存在点P,使得△ADP为等腰三角形,若存在,求出点P的坐标,若不存在,说明理由.
分析 (1)根据函数的关系式我们可求出A,B两点的坐标为(-4$\sqrt{3}$,0),(0,4),OA=4$\sqrt{3}$,OB=4,因此∠OAB=30°,因为三角形CAB是个等边三角形,因此∠CAB=60°,那么CA⊥OA,C点的横坐标就是A点的横坐标,如果求出CA的长那么就能求出C点的坐标了,根据AC=AB,有OA、OB的长,根据勾股定理我们可求出AB的长,也就求出AC的长,那么C点的坐标就求出来了.
(2)根据S△ABC=S△ABM,两三角形同底,也应该等高,因此M必在与AB平行的直线上,因此这条直线的斜率与已知的函数的斜率相同,可用C点坐标先确定MC所在直线的函数关系式,然后将M的坐标代入其中求出M的坐标.
(3)可分三种情况进行讨论即可求得.
解答 解:(1)根据直线的函数关系式,我们可得出A点的坐标为(-4$\sqrt{3}$,0),B点的坐标为(0,4),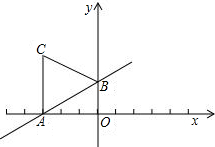
那么OA=4$\sqrt{3}$,OB=4,直角三角形ABO中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=8,∠BAO=30°,
根据三角形ABC是个等边三角形,因此∠CAB=60°.∠CAO=∠CAB+∠BAO=90°,
因此C点的横坐标应该和A点相同,
∵CA=AB=BC,
∴AC=AB=8,
那么C点的坐标为(-4$\sqrt{3}$,8).
(2)由题意可知,M必在与AB平行的直线上,
当M、C在直线AB同侧时,设这条直线为y=$\frac{\sqrt{3}}{3}$x+b,
将C点的坐标代入这条直线中得:-4+b=8,b=12,
因此这条直线的解析式是y=$\frac{\sqrt{3}}{3}$x+12
当M、C在直线AB的异侧时,y=$\frac{\sqrt{3}}{3}$x-4,
把y=2代入y=$\frac{\sqrt{3}}{3}$x+12得,$\frac{\sqrt{3}}{3}$m+12=2,m=-10$\sqrt{3}$,
把y=2代入y=$\frac{\sqrt{3}}{3}$x-4得,$\frac{\sqrt{3}}{3}$m-4=2,m=6$\sqrt{3}$,
因此M点的坐标为(-10$\sqrt{3}$,2)或(6$\sqrt{3}$,2),
(3)分三种情况: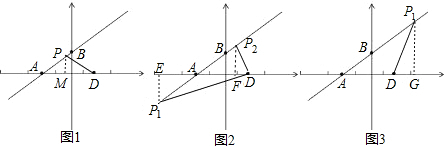
①以P为顶点,AP、DP为腰,图1,过P作PM⊥AD,PD就是线段AD的垂直平分线,AM=DM=2+2$\sqrt{3}$,
OM=DM-OD=2+2$\sqrt{3}$-4=2$\sqrt{3}$-2,那么P的横坐标就是2-2$\sqrt{3}$,代入函数式中即可求出P的坐标为(2-2$\sqrt{3}$,$\frac{2\sqrt{3}}{3}$+2),
此时P点的坐标是(2-2$\sqrt{3}$,$\frac{2\sqrt{3}}{3}$+2);
②以A为顶点,AP,AD为腰,如图2,过P1作P1E⊥x轴于E,由(1)知,∠BAO=30°,AP1=AD=4+4$\sqrt{3}$,
在直角三角形AP1E中,P1E=$\frac{1}{2}$AP1=2+2$\sqrt{3}$,AE=$\frac{\sqrt{3}}{2}$AP1=2$\sqrt{3}$+6,
∴P1(-6$\sqrt{3}$-6,-2$\sqrt{3}$-2),
同理:P2(6-2$\sqrt{3}$,2+2$\sqrt{3}$)
此时P点的坐标是(-6$\sqrt{3}$-6,-2$\sqrt{3}$-2)或(6-2$\sqrt{3}$,2+2$\sqrt{3}$);
③以D为顶点,AD,DP为腰,如图3,
同理证得PG=2$\sqrt{3}$+6,DG=2+2$\sqrt{3}$,
∴P点的坐标是(2$\sqrt{3}$+6,2$\sqrt{3}$+6),
因此存在这样的点P,且P的坐标为(2-2$\sqrt{3}$,$\frac{2\sqrt{3}}{3}$+2)或(-6$\sqrt{3}$-6,-2$\sqrt{3}$-2)或(6-2$\sqrt{3}$,2+2$\sqrt{3}$)或(2$\sqrt{3}$+6,2$\sqrt{3}$+6).
点评 本题综合考查了一次函数和直角三角形的应用,本题中利用直角三角形来求线段的长,从而得出点的坐标是解题的基本思路.要注意第三问中要把所有的情况都考虑到,不要遗漏任何一种情况.

| A. | 166×104 | B. | 1.66×105 | C. | 1.66×106 | D. | 0.166×107 |
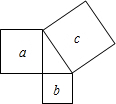 如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )
如图,a、b、c分别表示直角三角形的三边向外作的正方形的面积,下列关系正确的是( )| A. | a+b=c | B. | a2+b2=c2 | C. | ab=c | D. | a+b=c2 |
 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.
如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.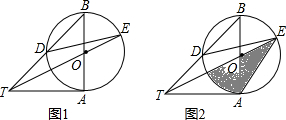
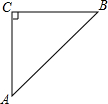 如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.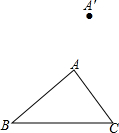 平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.
平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°. 如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为360度.
如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为360度.