题目内容
13．
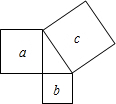如图，a、b、c分别表示直角三角形的三边向外作的正方形的面积，下列关系正确的是（ ）| A． | a+b=c | B． | a2+b2=c2 | C． | ab=c | D． | a+b=c2 |
分析 根据正方形的面积=边长×边长可表示出三个正方形的边长，结合勾股定理即可得出结论．
解答 解：由正方形的面积公式可知：
左边正方形的边长=$\sqrt{a}$，右边正方形的边长=$\sqrt{c}$，下边正方形的边长=$\sqrt{b}$，
由勾股定理可知：
$（\sqrt{a}）^{2}+（\sqrt{b}）^{2}=（\sqrt{c}）^{2}$，即a+b=c．
故选A．
点评 本题考查了正方形的面积公式以及勾股定理，解题的关键是表示出三个正方形的边长．本题属于基础题，难度不大，解决该题型题目时，根据数量关系利用勾股定理即可得出结论．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
12．若∠A和∠B的两边分别平行，且∠A比∠B的2倍少30°，则∠B的度数为（ ）
| A． | 30° | B． | 70° | C． | 30°或70° | D． | 100° |
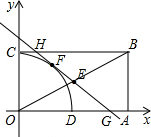如图，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，顶点A、C分别在x轴、y轴的正半轴上，且OA=2，OC=1，矩形对角线AC、OB相交于E，过点E的直线与边OA、BC分别相交于点G、H，以O为圆心，OC为半径的圆弧交OA于D，若直线GH与弧CD所在的圆相切于矩形内一点F，则下列结论：①AG=CH；②GH=$\frac{5}{3}$；③直线GH的函数关系式y=-$\frac{3}{4}x+\frac{5}{4}$；④梯形ABHG的内部有一点P，当⊙P与HG、GA、AB都相切时，⊙P的半径为$\frac{1}{4}$．其中正确的有（ ）
8．下列语句中，不是命题的是（ ）
| A． | 若两角之和为90°，则这两个角互余 | B． | 延长线段AO到点C，使OC=OA | ||
| C． | 平角是一条直线 | D． | 相等的角是对顶角 |
5．下列各组数中互为相反数的一组数是（ ）
| A． | |-2|与2 | B． | -2与-$\frac{1}{2}$ | C． | -2与$\root{3}{-8}$ | D． | -3与$\sqrt{（-3）^{2}}$ |
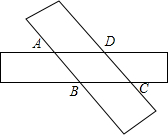如图，两张宽为1cm的矩形纸条交叉叠放，其中重叠部分部分是四边形ABCD，
3．将二次函数y=x2+1的图象向右平移1个单位，则平移后的二次函数的解析式为（ ）
| A． | y=x2 | B． | y=（x-1）2 | C． | y=（x-1）2+1 | D． | y=（x+1）2+1 |