题目内容
14.求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016,于是2S=2+22+23+…+22017,因此2S-S=22017-1,所以S=22017-1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )| A. | 52017-1 | B. | 52016-1 | C. | $\frac{{5}^{2017}-1}{4}$ | D. | $\frac{{5}^{2016}-1}{4}$ |
分析 仿照例子,设S=1+5+52+53+…+52016,由此可得出5S=5+52+53+…+52017,两者做差除以4即可得出S值,此题得解.
解答 解:设S=1+5+52+53+…+52016,则5S=5+52+53+…+52017,
∴5S-S=52017-1,
∴S=$\frac{{5}^{2017}-1}{4}$.
故选C.
点评 本题考查了规律型中的数字的变化类,解题的关键是仿照例子计算1+5+52+53+…+52016.本题属于基础题,难度不大,本题其实是等比数列的求和公式,但初中未接触过该方面的知识,需要借助于错位相减法来求出结论.

练习册系列答案
相关题目
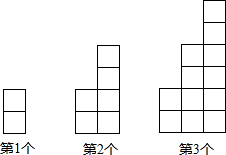 如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为n(n+1).
如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为n(n+1).