题目内容
17.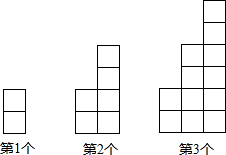 如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为n(n+1).
如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为n(n+1).
分析 设第n个图案中正方形的总个数为an,根据给定图案写出部分an的值,根据数据的变化找出变换规律“an=n(n+1)”,由此即可得出结论.
解答 解:设第n个图案中正方形的总个数为an,
观察,发现规律:a1=2,a2=2+4=6,a3=2+4+6=12,…,
∴an=2+4+…+2n=$\frac{n(2n+2)}{2}$=n(n+1).
故答案为:n(n+1).
点评 本题考查了规律型中的图形的变化类,解题的关键是找出变换规律“an=n(n+1)”.本题属于基础题,难度不大,根据给定图案写出部分图案中正方形的个数,根据数据的变化找出变化规律是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.一组数据8,3,8,6,7,8,7的众数和中位数分别是( )
| A. | 8,6 | B. | 7,6 | C. | 7,8 | D. | 8,7 |
14.求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016,于是2S=2+22+23+…+22017,因此2S-S=22017-1,所以S=22017-1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )
| A. | 52017-1 | B. | 52016-1 | C. | $\frac{{5}^{2017}-1}{4}$ | D. | $\frac{{5}^{2016}-1}{4}$ |
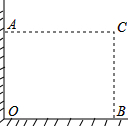 在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2. 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).