题目内容
1.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A($\frac{5}{3}$,0),B(0,4),则点B4的坐标为(20,4),点B2017的坐标为(10086,0).
分析 首先利用勾股定理得出AB的长,进而得出三角形的周长,进而求出B2,B4的横坐标,进而得出变化规律,即可得出答案.
解答 解:由题意可得:∵AO=$\frac{5}{3}$,BO=4,
∴AB=$\frac{13}{3}$,
∴OA+AB1+B1C2=$\frac{5}{3}$+$\frac{13}{3}$+4=6+4=10,
∴B2的横坐标为:10,B4的横坐标为:2×10=20,B2016的横坐标为:$\frac{2016}{2}$×10=10080,
∵B2C2=B4C4=OB=4,
∴点B4的坐标为(20,4),
∴B2017的横坐标为10080+$\frac{5}{3}$+$\frac{13}{3}$=10086,纵坐标为0,
∴点B2017的坐标为:(10086,0),
故答案为:(20,4)、(10086,0).
点评 此题主要考查了点的坐标以及图形变化类,根据题意得出B点横坐标变化规律是解题关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.关于二次函数y=-2x2+1,下列说法错误的是( )
| A. | 图象开口向下 | B. | 图象的对称轴为x=$\frac{1}{2}$ | ||
| C. | 函数最大值为1 | D. | 当x>1时,y随x的增大而减小 |
20.已知正方形ABCD,等边三角形PAQ,其中点P在BC上,点Q在CD上,则∠BAP=( )
| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
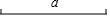 (1)如图,已知线段a,求作△ABC,使得AB=AC,BC=a,高AD=$\frac{1}{2}$a;
(1)如图,已知线段a,求作△ABC,使得AB=AC,BC=a,高AD=$\frac{1}{2}$a;